Theorie des Spannungsfalls
Im Folgenden werden die theoretischen Grundlagen zu den Spannungsverhältnissen und den sich einstellenden Spannungsfällen im Verteilungsnetz vorgestellt und aus deren mathematischer Beschreibung die möglichen Einflussgrößen abgeleitet. Eine gängige Methode Netzgrößen darzustellen ist die Verwendung von komplexen Zeigern, weil die Transformation der Größen aus dem Zeit- in den Frequenzbereich eine einfachere Berechnung und Darstellung des Netzzustandes ermöglicht. Auf diesem Weg soll im Weiteren der Spannungsfall erläutert werden.
Der komplexe Spannungsfall
In der Regel können Leitungen und Transformatoren vereinfacht als eine Reihenschaltung eines ohmschen Widerstandes ![]() und einer Reaktanz
und einer Reaktanz ![]() betrachtet werden. Abbildung 1 zeigt hierzu das Ersatzschaltbild (mit den auf die Länge
betrachtet werden. Abbildung 1 zeigt hierzu das Ersatzschaltbild (mit den auf die Länge ![]() normierten Impedanzgrößen
normierten Impedanzgrößen ![]() und
und ![]() ) sowie das Zeigerdiagramm der Spannungen. Ein Stromfluss
) sowie das Zeigerdiagramm der Spannungen. Ein Stromfluss ![]() über diese beiden Elemente führt zu einer Differenz der Spannung am Leitungsanfang
über diese beiden Elemente führt zu einer Differenz der Spannung am Leitungsanfang ![]() und der Spannung am Ende
und der Spannung am Ende ![]() in Betrag und Phase. Diesen Unterschied beschreibt der komplexe Spannungsfall
in Betrag und Phase. Diesen Unterschied beschreibt der komplexe Spannungsfall ![]() , der sich aus dem Produkt der Impedanz
, der sich aus dem Produkt der Impedanz ![]() und dem Strom
und dem Strom ![]() errechnet.
errechnet. ![]() kann auf die beiden Ersatzschaltbildelemente aufgeteilt (
kann auf die beiden Ersatzschaltbildelemente aufgeteilt (![]() und
und ![]() ) oder in seinen Real- und Imaginärteil zerlegt werden. Der Realteil von
) oder in seinen Real- und Imaginärteil zerlegt werden. Der Realteil von ![]() wird als Längsspannungsfall
wird als Längsspannungsfall ![]() und der Imaginärteil von
und der Imaginärteil von ![]() als Querspannungsfall
als Querspannungsfall ![]() bezeichnet. Für die Netzplanung ist streng genommen der Spannungsunterschied der Effektivwerte am Anfang und am Ende der Leitung
bezeichnet. Für die Netzplanung ist streng genommen der Spannungsunterschied der Effektivwerte am Anfang und am Ende der Leitung ![]() und nicht
und nicht ![]() oder
oder ![]() entscheidend. Aus Abbildung 1 wird ersichtlich, dass auf der einen Seite im Vergleich zum eigentlichen auslegungsrelevanten Spannungsfall
entscheidend. Aus Abbildung 1 wird ersichtlich, dass auf der einen Seite im Vergleich zum eigentlichen auslegungsrelevanten Spannungsfall ![]() der Spannungsfall über der Netz- bzw. Transformatorimpedanz
der Spannungsfall über der Netz- bzw. Transformatorimpedanz ![]() stets größer ist, auf der anderen Seite sein Realteil, der betragsmäßige Längsspannungsfall
stets größer ist, auf der anderen Seite sein Realteil, der betragsmäßige Längsspannungsfall ![]() geringfügig kleiner ist. Bei kleinen Verdrehwinkeln
geringfügig kleiner ist. Bei kleinen Verdrehwinkeln ![]() zwischen
zwischen ![]() und
und ![]() , was für die Mittel- und Niederspannungsebene zutrifft, kann aber in guter Näherung der Längsspannungsfall
, was für die Mittel- und Niederspannungsebene zutrifft, kann aber in guter Näherung der Längsspannungsfall ![]() auf Leitungen mit
auf Leitungen mit ![]() gleich gesetzt werden. Bei genauerer Betrachtung ergeben sich in der Praxis Unterschiede zwischen
gleich gesetzt werden. Bei genauerer Betrachtung ergeben sich in der Praxis Unterschiede zwischen ![]() und
und ![]() von 0,1 bis zu 2,5 %, bezogen auf
von 0,1 bis zu 2,5 %, bezogen auf ![]() . Bei Transformatoren ergeben sich aufgrund der stark induktiv geprägten Impedanz deutlich größere Unterschiede.
. Bei Transformatoren ergeben sich aufgrund der stark induktiv geprägten Impedanz deutlich größere Unterschiede.
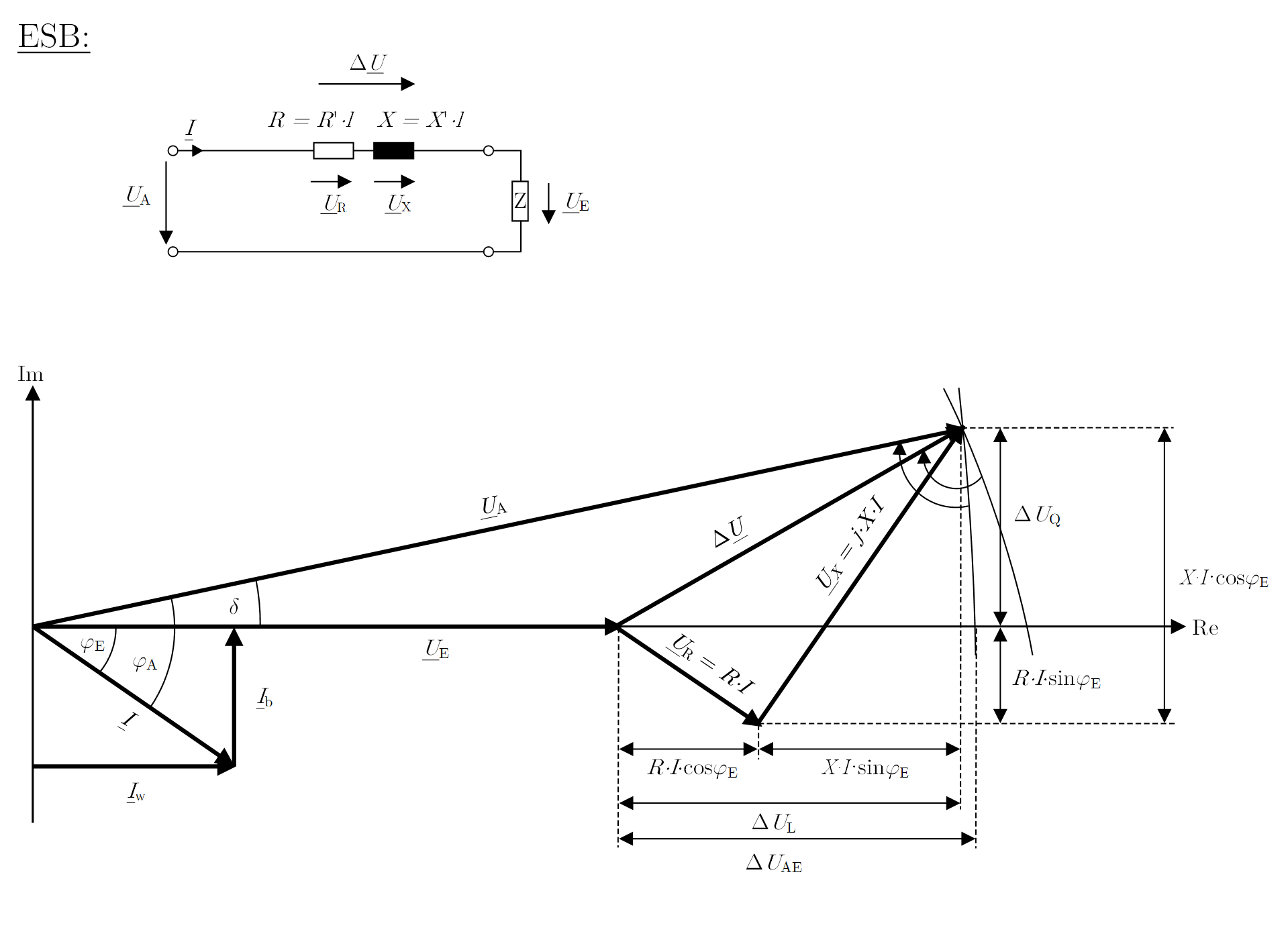
Nachfolgend werden die mathematischen Zusammenhänge der jeweiligen Spannungsfallkomponenten unter Annahme eines Stroms in Bezugspfeilrichtung (Richtung ![]() ) und unter Verwendung eines induktiven Blindstroms dargestellt. Die aufgezeigten Formeln haben allerdings allgemeine Gültigkeit. Kapazitiver Blindstrom oder Stromfluss entgegen des Bezugspfeils aus Abbildung 1 müssen lediglich mit negativen Vorzeichen eingesetzt werden.
) und unter Verwendung eines induktiven Blindstroms dargestellt. Die aufgezeigten Formeln haben allerdings allgemeine Gültigkeit. Kapazitiver Blindstrom oder Stromfluss entgegen des Bezugspfeils aus Abbildung 1 müssen lediglich mit negativen Vorzeichen eingesetzt werden.
Vereinfachend kann also der auslegungsrelevante Spannungsfall in Form des Längsspannungsfalls berechnet werden, wenn man den Verschiebungsfaktor in obiger Gleichung zur Berechnung des Spannungsfalls ![]() , der als Phasengröße mit
, der als Phasengröße mit ![]() gekennzeichnet wird, ausklammert:
gekennzeichnet wird, ausklammert:
und einen auf die Leitungslänge normierten Längswiderstand ![]() einführt:
einführt:
erhält man:
Darin ist ![]() die Drehstrom-Wirkleistung und
die Drehstrom-Wirkleistung und ![]() die verkettete Spannung am Leitungsende. Die übrigen Größen können der Abbildung 1 entnommen werden. Die Leiter-Leiter-Größe errechnet sich aus der Phasengröße über die Multiplikation mit dem Verkettungsfaktor
die verkettete Spannung am Leitungsende. Die übrigen Größen können der Abbildung 1 entnommen werden. Die Leiter-Leiter-Größe errechnet sich aus der Phasengröße über die Multiplikation mit dem Verkettungsfaktor ![]() :
:
Üblicherweise wird die Nennspannung für die in der Regel unbekannte Spannung ![]() eingesetzt und damit begründet, dass beide Spannungen maximal um
eingesetzt und damit begründet, dass beide Spannungen maximal um ![]() voneinander abweichen. Normiert auf die Nennspannung ergibt sich der relative Spannungsfall:
voneinander abweichen. Normiert auf die Nennspannung ergibt sich der relative Spannungsfall:
Der komplexe Spannungsfall im Verteilungsnetz
Auf Basis der gewonnenen Erkenntnisse kann der Spannungsfall entlang der in Abbildung 2 dargestellten Übertragungsstrecke als Addition einzelner Spannungsfälle längs der Betriebsmittel aufgefasst werden.
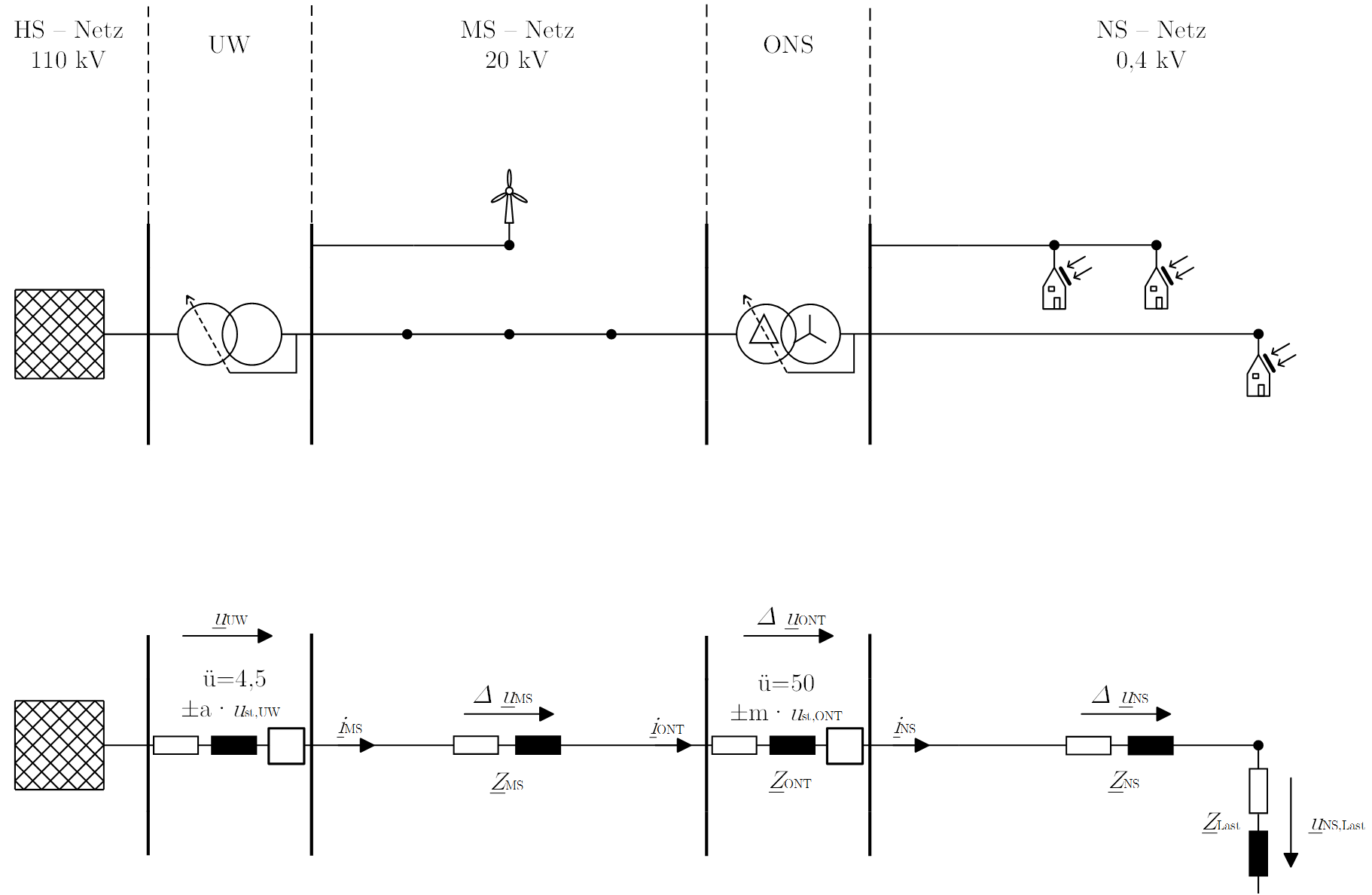
Um die Spannungsfälle im MS- und NS-Netz einheitlich in einem Diagramm darstellen zu können, werden diese im Folgenden auf die jeweilige Nennspannung normiert:
Der Ortsnetztransformator wird dabei von der Oberspannungsseite her betrachtet und die Impedanz entsprechend der MS zugeordnet.
Ausgehend von der Spannung ![]() am UW, die in der Regel maximal um die halbe Regelbandbreite (Die RBB ergibt sich aus den eingestellten Parametern für die obere und untere Schaltschwelle
am UW, die in der Regel maximal um die halbe Regelbandbreite (Die RBB ergibt sich aus den eingestellten Parametern für die obere und untere Schaltschwelle ![]() und
und ![]() , die üblicherweise symmetrisch um den Sollwert gelegt werden) vom Sollwert (SW) abweichen kann, ergibt sich im Starklastfall eine minimale Spannung
, die üblicherweise symmetrisch um den Sollwert gelegt werden) vom Sollwert (SW) abweichen kann, ergibt sich im Starklastfall eine minimale Spannung ![]() aus der geometrischen Additon der Spannungsfälle auf der MS-Leitung (
aus der geometrischen Additon der Spannungsfälle auf der MS-Leitung (![]() ), über dem Ortsnetztransformator (
), über dem Ortsnetztransformator (![]() ) und entlang der Niederspannungsleitung (
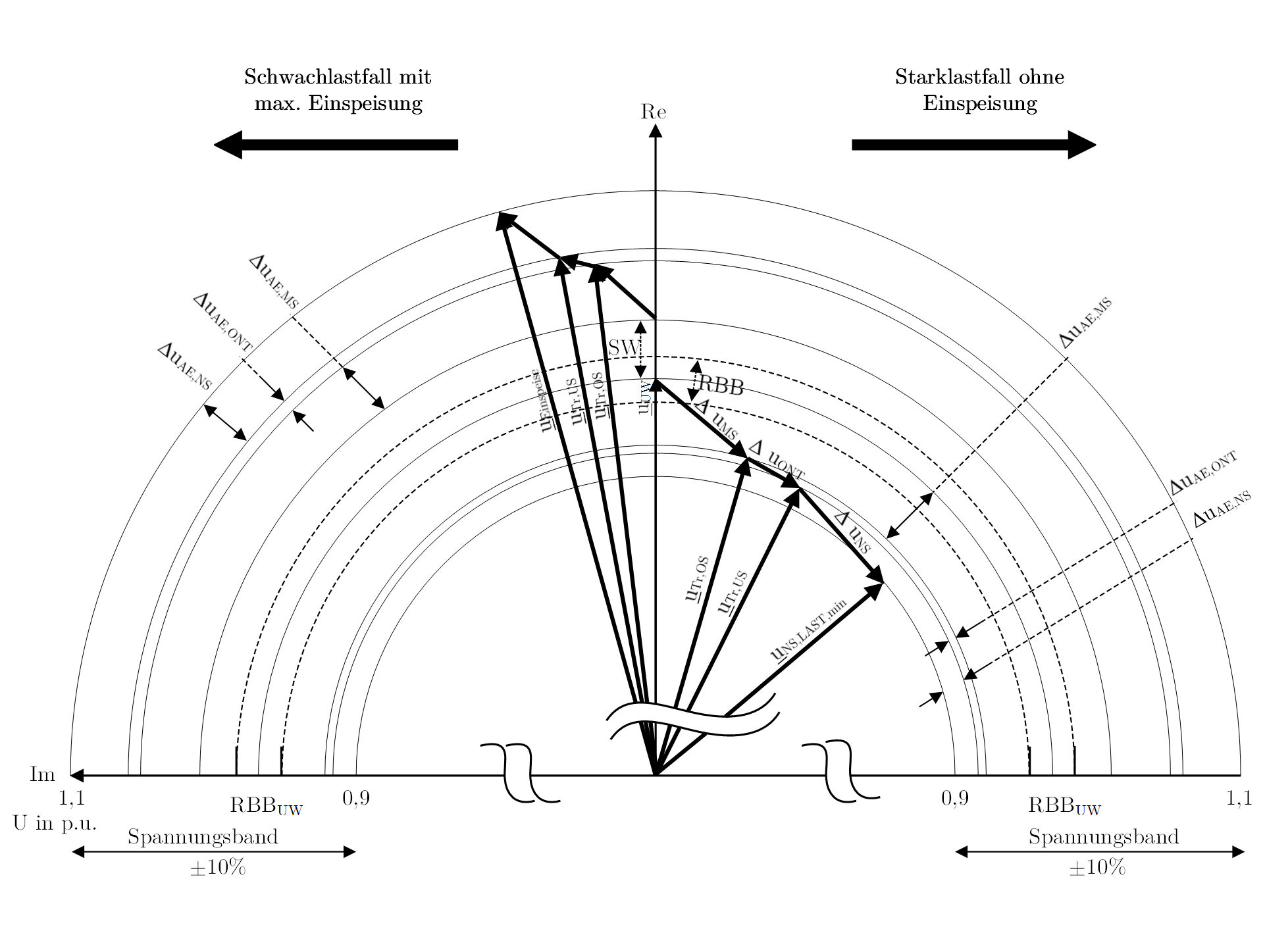
) und entlang der Niederspannungsleitung (![]() ). Das resultierende verkettete Spannungszeigerdiagramm ist in Abbildung 3 im rechten Bildteil zu sehen. Zudem ist eine Projektion der wirksamen Spannungsunterschiede auf das zulässige Spannungsband (
). Das resultierende verkettete Spannungszeigerdiagramm ist in Abbildung 3 im rechten Bildteil zu sehen. Zudem ist eine Projektion der wirksamen Spannungsunterschiede auf das zulässige Spannungsband (![]() ) dargestellt (Schnittpunkt der Kreise mit horizontaler Linie). Des Weiteren ist die Regelbandbreite des Umspannwerk-Transformators eingezeichnet, innerhalb deren die Spannung der MS-Sammelschiene schwanken kann. Für den Starklastfall ohne Einspeisung ist deshalb von einer an der unteren Schwelle der Regelbandbreite liegenden MS-Sammelschienenspannung
) dargestellt (Schnittpunkt der Kreise mit horizontaler Linie). Des Weiteren ist die Regelbandbreite des Umspannwerk-Transformators eingezeichnet, innerhalb deren die Spannung der MS-Sammelschiene schwanken kann. Für den Starklastfall ohne Einspeisung ist deshalb von einer an der unteren Schwelle der Regelbandbreite liegenden MS-Sammelschienenspannung ![]() auszugehen. Dabei muss trotz maximal möglicher Spannungsfälle sichergestellt sein, dass die untere Spannungsbandgrenze von
auszugehen. Dabei muss trotz maximal möglicher Spannungsfälle sichergestellt sein, dass die untere Spannungsbandgrenze von ![]() nicht unterschritten wird. Auf der anderen Seite (linker Bereich in Abbildung 3) darf die Spannung an keinem Punkt im Verteilungsnetz über
nicht unterschritten wird. Auf der anderen Seite (linker Bereich in Abbildung 3) darf die Spannung an keinem Punkt im Verteilungsnetz über ![]() liegen. Maßgebend ist hierfür der Schwachlastfall mit maximaler Einspeisung aus dezentralen Erzeugungsanlagen mit einer anzunehmenden MS-Sammelschienenspannung an der oberen Schwelle der Regelbandbreite.
liegen. Maßgebend ist hierfür der Schwachlastfall mit maximaler Einspeisung aus dezentralen Erzeugungsanlagen mit einer anzunehmenden MS-Sammelschienenspannung an der oberen Schwelle der Regelbandbreite.
Bei Betrachtung von Abbildung 5 wird deutlich, dass die geometrische Lage der einzelnen Spannungsfälle entscheidenden Einfluss auf den letztendlich relevanten Spannungsunterschied ![]() hat (
hat (![]() ). Dieser Effekt ist vor allem bei Ortsnetztransformatoren (
). Dieser Effekt ist vor allem bei Ortsnetztransformatoren (![]() ) ersichtlich. Während der komplexe Spannungsfall (
) ersichtlich. Während der komplexe Spannungsfall (![]() ) entsprechend seiner relativen Kurzschlussspannung beträchtlich sein kann, z. B.
) entsprechend seiner relativen Kurzschlussspannung beträchtlich sein kann, z. B. ![]() bei einer Belastung mit Nennstrom und einem
bei einer Belastung mit Nennstrom und einem ![]() , wird mit ca.
, wird mit ca. ![]() ein wesentlich kleinerer Teil des Spannungsbandes effektiv belegt.
ein wesentlich kleinerer Teil des Spannungsbandes effektiv belegt.
Die in der komplexen Ebene beschriebenen Zusammenhänge können mathematisch ausgedrückt werden:
Die Kleinbuchstaben ![]() kennzeichnen die auf die jeweilige Nennspannung normierten Spannungen bzw. Spannungsfälle. Die Buchstaben
kennzeichnen die auf die jeweilige Nennspannung normierten Spannungen bzw. Spannungsfälle. Die Buchstaben ![]() und
und ![]() nehmen ganzzahlige Werte an und symbolisieren die automatische Spannungsregelung über Stufenschalter bzw. die manuelle Einstellung über Umsteller. Der Index 4 bzw. 6 repräsentiert die Netzebene, in der sich die Spannungsregel-/einstelleinrichtung befindet (siehe Tabelle 1).
nehmen ganzzahlige Werte an und symbolisieren die automatische Spannungsregelung über Stufenschalter bzw. die manuelle Einstellung über Umsteller. Der Index 4 bzw. 6 repräsentiert die Netzebene, in der sich die Spannungsregel-/einstelleinrichtung befindet (siehe Tabelle 1).
Tabelle 1: Legende zum Index der Spannungsgleichung
![Rendered by QuickLaTeX.com \begin{tabular}{|r|ll|} \hline \rowcolor[gray]{.9} Index & Netzebene & \\ \hline 1 & Netzebene 1: & Höchstspannungsebene 220/380 kV \\ 2 & Netzebene 2: & HöS-/HS-Verknüpfungspunkt \\ 3 & Netzebene 3: & Hochspannungsebene 110 kV \\ 4 & Netzebene 4: & HS-/MS-Verknüpfungspunkt (UW-Transformator) \\ 5 & Netzebene 5: & Mittelspannungsebene 10...30 kV \\ 6 & Netzebene 6: & MS-/NS-Verknüpfungspunkt (ONT) \\ 7 & Netzebene 7: & Niederspannungsebene U_n \le 1 kV \\ \hline \end{tabular}](https://ront.info/wp-content/ql-cache/quicklatex.com-fb67efb7f0e5edcdaab1d04aedec9e5f_l3.png)
Mit ![]() kann also eine Abweichung vom Nennübersetzungsverhältnis des Ortsnetztransformators berücksichtigt werden. Dies lässt sich in diskreten Stufen mit einer wirksamen Stufenspannung
kann also eine Abweichung vom Nennübersetzungsverhältnis des Ortsnetztransformators berücksichtigt werden. Dies lässt sich in diskreten Stufen mit einer wirksamen Stufenspannung ![]() im spannungslosen Zustand verändern. Dabei ist zu beachten, dass eine Verstellung des Übersetzungsverhältnisses das Niveau der Ausgangsspannung sowohl für den Last- als auch für den Einspeisefall gleichermaßen entsprechend erhöht bzw. erniedrigt. Der Term
im spannungslosen Zustand verändern. Dabei ist zu beachten, dass eine Verstellung des Übersetzungsverhältnisses das Niveau der Ausgangsspannung sowohl für den Last- als auch für den Einspeisefall gleichermaßen entsprechend erhöht bzw. erniedrigt. Der Term ![]() steht für die automatische Ausregelung des mit Nennübersetzung auf die Sekundärseite des UW-Transformators übertragene Hochspannung
steht für die automatische Ausregelung des mit Nennübersetzung auf die Sekundärseite des UW-Transformators übertragene Hochspannung ![]() . In Abbildung 4 ist das normierte Spannungszeigerdiagramm für den Lastfall dargestellt. Mit den blauen Pfeilen sind die UW-Regelung und die Einstellbarkeit des ONT-Übersetzungsverhältnisses angedeutet.
. In Abbildung 4 ist das normierte Spannungszeigerdiagramm für den Lastfall dargestellt. Mit den blauen Pfeilen sind die UW-Regelung und die Einstellbarkeit des ONT-Übersetzungsverhältnisses angedeutet.

Ersetzt man die jeweiligen Spannungsfälle durch deren Produkt aus Strom (weiterhin induktiver Blindstrom bzw. Blindleistung angenommen) und auf die Leitungslänge normierte Impedanz und drückt man die Wirk- und Blindanteile der Ströme durch die transportierte Leistung ![]() und
und ![]() aus, kann folgender Ausdruck gewonnen werden:
aus, kann folgender Ausdruck gewonnen werden:
Aus dieser Gleichung können alle grundsätzlichen Einflussmaßnahmen auf die Spannungshaltung abgeleitet werden. Diese sind:
Einflussmaßnahmen auf die Spannungshaltung
Impedanzreduktion
Die Impedanzreduktion zielt auf eine Verringerung der wirksamen Netz bzw. Transformatorimpedanz bestehend aus ![]() und
und ![]() . Mögliche Maßnahmen sind der Einbau paralleler Leitungen, Verwendung von Leitungen größeren Querschnitts, die Vermaschung von Netzteilen, Verringerung der effektiven Impedanzbeläge
. Mögliche Maßnahmen sind der Einbau paralleler Leitungen, Verwendung von Leitungen größeren Querschnitts, die Vermaschung von Netzteilen, Verringerung der effektiven Impedanzbeläge ![]() und
und ![]() , zusätzliche Ortsnetzstationen bzw. Umspannwerke (Verkürzung der Leitungslängen) oder die Verwendung einer größeren Transformatorbraureihe (
, zusätzliche Ortsnetzstationen bzw. Umspannwerke (Verkürzung der Leitungslängen) oder die Verwendung einer größeren Transformatorbraureihe (![]() ).
).
Wirkleistungsreduktion
Die Wirkleistungsreduktion beeinflusst in gleicher Weise wie die Impedanzreduktion den Spannungsfall längs der Netzbetriebsmittel. Die Absenkung der zu übertragenden Wirkleistung (![]() ) kann über Speicher, Spitzenkappung bei dezentralen Erzeugungsanlagen sowie Last- und Einspeisemanagement erreicht werden.
) kann über Speicher, Spitzenkappung bei dezentralen Erzeugungsanlagen sowie Last- und Einspeisemanagement erreicht werden.
Blindleistungsmanipulation
Durch Blindleistungsmanipulation kommt es neben der Beeinflussung der Länge des komplexen Spannungsfalls auch zu einer Drehung der Phasenlage. Induktiver Blindleistungsbezug wirkt spannungssenkend, kapazitiver spannungsanhebend. Eine Manipulation der Blindleistungsflüsse (![]() ) ist über Kompensationsanlagen (z. B. Kapazitäten, Drosseln, Leistungselektronik) oder Erzeugungsanlagen (z. B. Spannungsblindleistungsregelung durch PV-Wechselrichter, Synchrongeneratoren) aber auch Lasten (z. B. Synchronmaschinen im Phasenschieberbetrieb) und umrichterbasierten Speichern möglich.
) ist über Kompensationsanlagen (z. B. Kapazitäten, Drosseln, Leistungselektronik) oder Erzeugungsanlagen (z. B. Spannungsblindleistungsregelung durch PV-Wechselrichter, Synchrongeneratoren) aber auch Lasten (z. B. Synchronmaschinen im Phasenschieberbetrieb) und umrichterbasierten Speichern möglich.
Einsatz direkter Spannungsquellen
Unter diesem Begriff werden Gerätschaften (i. d. R. auf dem Transformatorprinzip beruhend) zusammengefasst, die durch eine „Zusatzspannung“ das Spannungsniveau beeinflussen. Im Verteilungsnetz findet man typischerweise Längsregler, d. h. es wird nur der Betrag der Spannung und nicht die Phasenlage verändert – der Einfluss wirkt längs des komplexen Spannungszeigers eines Netzknotens (z. B. ![]() ). Im Übertragungsnetz werden auch Quer- und Schrägregler verwendet um durch die zusätzliche Manipulation der Phasenlage die Leistungsflüsse im Stromnetz besser steuern zu können. Standardmäßig sind in jedem Verteilungsnetz zwei solcher direkter Spannungsquellen vorzufinden – der Umspannwerktransformator samt Stufenschalter und der Ortsnetztransformator mit integriertem Umsteller. So lässt sich die Aufnahmefähigkeit des Netzes für dezentrale Erzeugungsleistung erhöhen, indem man in die UW-Regelung eine dynamische Sollwertanpassung implementiert oder den ONT-Umsteller in den kritischen Netzbereichen saisonal den Gegebenheiten anpasst. Zusätzlich kann das Spannungsniveau über heute so bezeichnete Einzelstrangregler in der MS- oder NS-Leitung beeinflusst werden. Hierbei wird immer nur der nachfolgende Netzabschnitt beeinflusst. Eine weitere Lösungsmaßnahme ist der regelbare Ortsnetztransformator. Mit ihm kann ein komplettes Ortsnetz, bei höherer und geeigneter Installationsdichte auch Teile des MS-Netzes „entspannt“ werden.
). Im Übertragungsnetz werden auch Quer- und Schrägregler verwendet um durch die zusätzliche Manipulation der Phasenlage die Leistungsflüsse im Stromnetz besser steuern zu können. Standardmäßig sind in jedem Verteilungsnetz zwei solcher direkter Spannungsquellen vorzufinden – der Umspannwerktransformator samt Stufenschalter und der Ortsnetztransformator mit integriertem Umsteller. So lässt sich die Aufnahmefähigkeit des Netzes für dezentrale Erzeugungsleistung erhöhen, indem man in die UW-Regelung eine dynamische Sollwertanpassung implementiert oder den ONT-Umsteller in den kritischen Netzbereichen saisonal den Gegebenheiten anpasst. Zusätzlich kann das Spannungsniveau über heute so bezeichnete Einzelstrangregler in der MS- oder NS-Leitung beeinflusst werden. Hierbei wird immer nur der nachfolgende Netzabschnitt beeinflusst. Eine weitere Lösungsmaßnahme ist der regelbare Ortsnetztransformator. Mit ihm kann ein komplettes Ortsnetz, bei höherer und geeigneter Installationsdichte auch Teile des MS-Netzes „entspannt“ werden.
Nachfolgende Tabelle fasst die vier Kategorien mit den jeweiligen Lösungsmaßnahmen zur Behebung von Spannungsbandproblemen zusammen.
![Rendered by QuickLaTeX.com \begin{tabular}{||p{5 cm}|p{5 cm}|p{5 cm}|p{5 cm}||} \hline \hline \rowcolor[gray]{.9} \textbf{Impedanz} & \textbf{Wirkleistung} & \textbf{Blindleistung} & \textbf{Spannungstransformation} \\ \hline Stationsdichte\newline UW/ONS & Lastmanagement/\newline Demand-Side-Management & Q-fähige\newline Erzeugungsanlagen & Dynamische\newline Sollwertanpassung\newline UW-Transformator \\ \hline Leitungstausch/\newline Parallelverkabelung & Einspeisemanagement & eigene\newline Kompensationsanlagen & Zwischentransformation\newline MS-/NS-Strang \\ \hline Vermaschung/\newline Trennstellenverlagerung & Lastflusssteuerung & fremde\newline Kompensationsanlagen & Anpassung\newline Umsteller ONT \\ \hline Bemessungsleistung ONT & Zwischenspeicherung & Q-fähige\newline Speicher & Regelbarer\newline Ortsnetztransformator\\ \hline \hline \end{tabular}](https://ront.info/wp-content/ql-cache/quicklatex.com-3740aadecc71495ccbc79ef230a0c72b_l3.png)
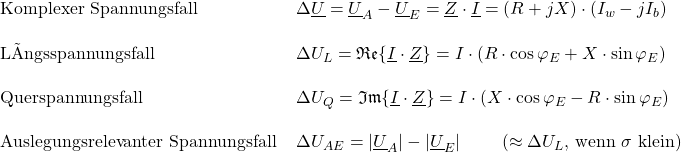
![Rendered by QuickLaTeX.com \begin{tabular}{rllll} $\underline{u}_{Last}$ & $= \underline{u}_{UW}\pm {\color{green} \underline {{\color{black} a_4\cdot \underline{u}_{St,UW}}}} $ & & & UW \\ & $- \Big[ \big( {\color{blue} \underline{{\color{black}P_{MS}}}} \cdot {\color{magenta} \underline{{\color{black} R'_{MS} \cdot l_{MS}}}} - {\color{red} \underline {{\color{black}Q_{MS}}}} \cdot {\color{magenta} \underline{{\color{black}X'_{MS} \cdot l_{MS}}}} \big)$ & $+ \quad j\; \big( P_{MS} \cdot X'_{MS} \cdot l_{MS} + Q_{MS} \cdot R'_{MS} \cdot l_{MS} \big) \Big]$ & $\cdot \; \frac{1}{\sqrt{3} \cdot U^2_{n,MS}}$ & MS-Leitung \\ %============================== &&&&\\ & $\pm\; {\color{green} \underline {{\color{black}m_6 \cdot \underline{u}_{St,ONT}}}}$ & & & \\ % &&&&\\ & $- \Big[ \big({\color{blue} \underline {{\color{black} P_{ONT}}}} \cdot {\color{magenta} \underline {{\color{black}R_{ONT}}}} - {\color{red} \underline {{\color{black}Q_{ONT}}}} \cdot {\color{magenta} \underline {{\color{black}X_{ONT}}}} \big)$ & $+ \quad j\; \big(P_{ONT} \cdot X_{ONT} + Q_{ONT} \cdot R_{ONT} \big) \Big] $ & $\cdot \; \frac{1}{\sqrt{3} \cdot U^2_{n}}$ & ONT \\ %============================== &&&&\\ & $- \Big[ \big( {\color{blue} \underline {{\color{black} P_{NS}}}} \cdot {\color{magenta} \underline {{\color{black}R'_{NS} \cdot l_{NS}}}} - {\color{red} \underline {{\color{black}Q_{NS}}}} \cdot {\color{magenta} \underline {{\color{black}X'_{NS} \cdot l_{NS}}}} \big)$ & $+ \quad j\; \big( P_{NS} \cdot X'_{NS} \cdot l_{NS} + Q_{NS} \cdot R'_{NS} \cdot l_{NS} \big) \Big]$ & $\cdot \; \frac{1}{\sqrt{3} \cdot U^2_{n,NS}}$ & NS-Leitung \\ %============================== &&&&\\ &&&&\\ & Längsspannungsfall $\Delta U_L$ & Querspannungsabfall $\Delta U_Q$ & Normierung &\\ \end{tabular}](https://ront.info/wp-content/ql-cache/quicklatex.com-c49e5d4fcfcf65783789ae93a7c5cd6b_l3.png)