Regelstrategien - Informationsportal regelbare Ortsnetztransformatoren

Analog zu den etablierten und derzeit in Entwicklung befindlichen Regelstrategien für UW-Transformatoren sind für RONT verschiedene Regelvarianten denkbar. Im Unterschied zur UW-Regelung weisen die Leistungsflüsse und somit Spannungsverhältnisse am RONT bzw. in Ortsnetzen eine deutlich größere Volatilität auf. Hinzu kommt, dass in der Regel in der MS- und NS-Ebene nicht standardmäßig Messeinrichtungen mit ausreichend hoher Zeitauflösung und Verfügbarkeit/Erreichbarkeit vorhanden sind, die Eingangsdaten für eine Regelung bereitstellen könnten. In den folgenden Abschnitten wird zunächst die Standard-Sammelschienenregelung erläutert, danach auf offene Potentiale eingegangen und darauf aufbauende alternative Regelkonzepte dargelegt.

Standard-Sammelschienenregelung

RONT werden i. d. R. mit der Standard-Sammelschienenregelung betrieben. Diese Art der Regelung wird derzeit auch größtenteils in Leistungstransformatoren verwendet. Grund für die mehrheitliche Nutzung ist die vergleichsweise einfache Implementierung im Regler, sowie die wenig aufwändige Messinfrastruktur, welche im Prinzip aus einem Spannungsmessgerät an der Sammelschiene und der Kabelverbindung zum Spannungsregler besteht. Bei der Standard-Sammelschienenregelung wird der Spannungswert an der NS-Sammelschiene an bis zu drei Phasen gemessen (siehe Abbildung 1). Erfolgt die Messung an weniger als drei Phasen, muss für die Unsymmetrie der Phasenspannungen ein Worst-Case-Wert, wie er beispielsweise mit 2 % in [DIN EN 50160] angegeben ist, berücksichtigt werden. Somit wird sichergestellt, dass keine Phasenspannung bei hoher Unsymmetrie außerhalb des zulässigen Spannungsbandes liegt.

Die eigentliche Regelung basiert auf einem Soll-Ist-Wert-Vergleich, bei dem überprüft wird ob der Augenblickswert innerhalb eines Regelbandes liegt. Werden die Grenzen des Regelbandes verletzt, wird eine Schalthandlung initiiert, die den Spannungswert um eine Stufenspannung anhebt bzw. absenkt.

Die Lage des Regelbandes wird dabei über die Vorgabe des Sollwertes und dessen zulässige positive und negative Abweichung definiert. Typischerweise liegt das Regelband symmetrisch um den Sollwert. Abbildung 2 zeigt hierzu eine vereinfachte Darstellung. An den Zeitpunkten $t_1$ und $t_2$ finden Schalthandlungen des RONT statt.

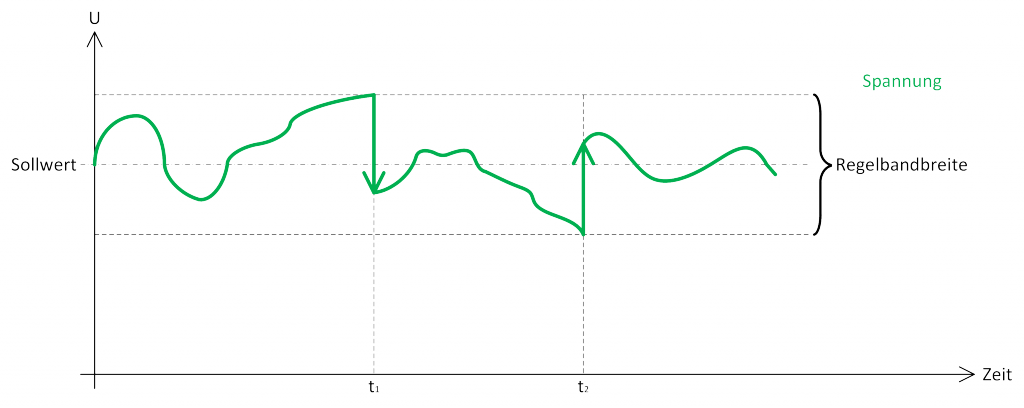
Abbildung 2: Schalthandlungen des RONT (vereinfacht)

Zur Minimierung der Anzahl an Schalthandlungen kann je nach Regelungssystem über zwei Varianten eine Totzeit in den Regelalgorithmus eingebunden werden. Beim linearen Regelverhalten wird eine Schalthandlung ausgelöst, nachdem das Regelband verlassen wurde und ein Timer abgelaufen ist. Beim integralen Regelverhalten reagiert der Spannungsregler mit einer variablen Verzögerungszeit. Das bedeutet, je größer die Regelabweichung ist, desto schneller wird die Schalthandlung angestoßen.

Abbildung 3: Band für Spannungsanhebung, bzw. Band für Spannungsfall

An dieser Stelle sei nochmals angemerkt, dass diese Art der Regelung das Ziel verfolgt, die von der MS-Ebene herrührenden Spannungsschwankungen auszuregeln und dadurch das Spannungsniveau an der NS-Sammelschiene des RONT innerhalb eines definierten Regelbandes konstant zu halten. Es wird nicht das Ziel verfolgt Spannungsanhebungen in der NS-Ebene entgegenzuwirken.

Vielmehr hat die Ausregelung der MS-Schwankung den Effekt, dass eine größere Spannungsanhebung in der NS-Ebene zugelassen werden kann, da sich die Schwankungen der MS-Ebene nicht ins NS-Netz durchsetzen können. Auf Seiten der Netzplanung wird über die Wahl des Spannungssollwertes bzw. die Lage des Regelbandes definiert, wie das verfügbare Spannungsband (1,10 p.u. – 0,90 p.u. – Regelband) auf Spannungsanhebung und Spannungsfall aufgeteilt wird (siehe Abbildung 3).

Offene Potentiale

Die Standard-Sammelschienenregelung ist eine robuste Regelungsvariante, die es der Netzplanung durch die Gewährleistung eines definierten Spannungsbandes an der NS-Seite des RONT erlaubt, das Spannungsband im Verteilungsnetz höher auszunutzen. Dies birgt bereits große Potentiale, die beispielsweise ein deutliches Plus an anschließbaren EZA ermöglicht, aber auch die Aufteilung auf Verbraucher und Erzeuger ist möglich.

Für die Wahl der Lage des Regelbandes werden i. d. R. Worst-Case-Szenarien verwendet. D. h. es werden der Einspeise- und der Starklastfall betrachtet und die entsprechende Spannungsanhebung und der Spannungsfall definieren die Lage des Regelbandes. Auf Basis dieser Planung können beide Fälle gleichzeitig eintreten ohne dass das Spannungsband verletzt wird. D. h. es kann sowohl in einem Strang der Einspeisefall und in einem anderen zeitgleich der Starklastfall vorliegen.

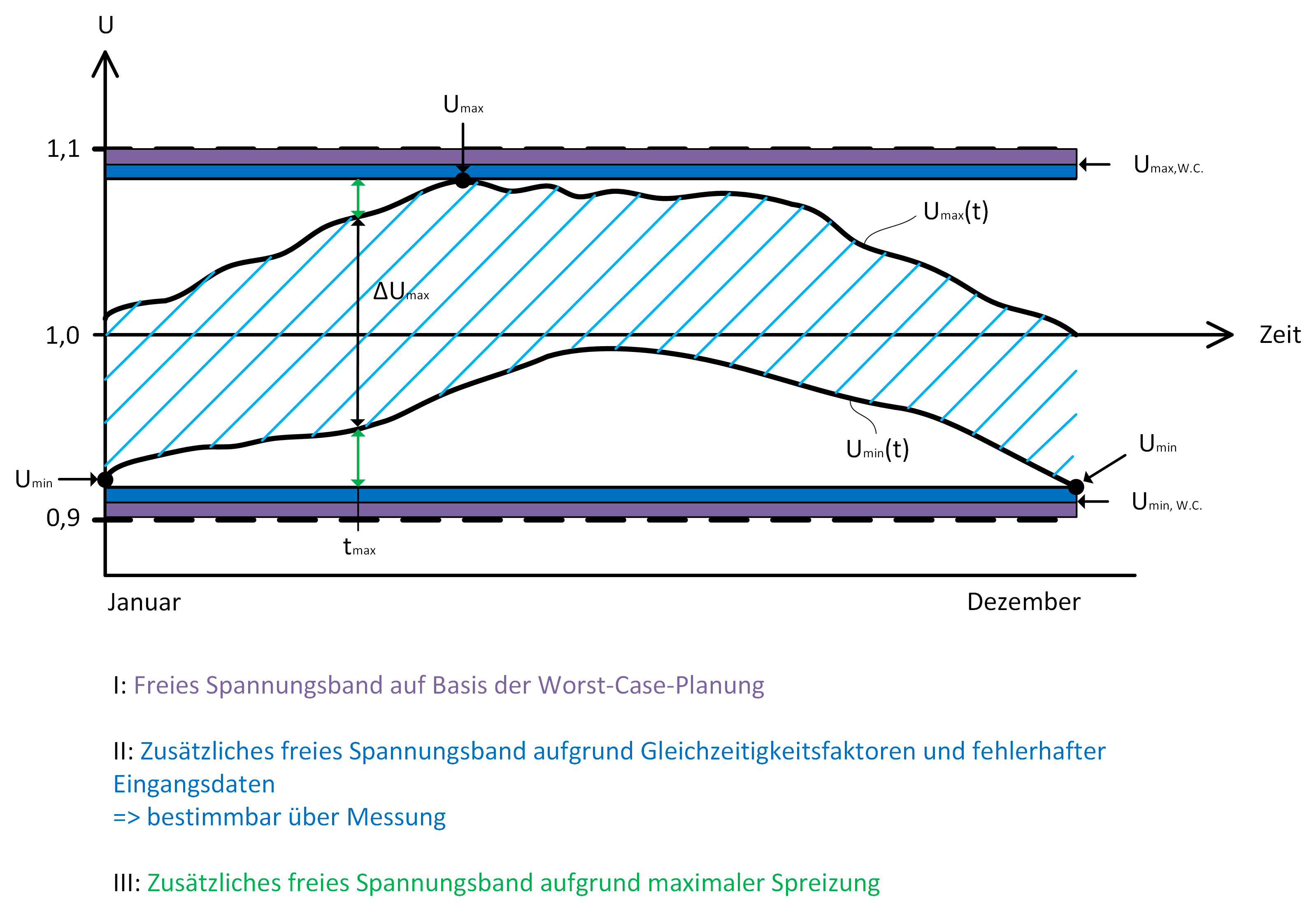
Betrachtet man das Spannungsband, wie beispielhaft in Abbildung 4 dargestellt, so ergeben sich verschiedene Potentiale die zusätzlich gehoben werden könnten. Dargestellt ist ein prinzipieller zeitlicher Verlauf des NS-seitig belegten Spannungsbandes. Dieses ergibt sich durch Betrachtung der minimal $U_{min}(t)$ und maximal $U_{max}(t)$ auftretenden Spannung an allen vorhandenen Netzknoten zu jedem Zeitpunkt des Jahres. Die minimalen Spannungsabstände zu den Grenzwerten ergeben sich über zwei Bereiche. Bereich I beschreibt das freie Spannungsband, das sich auf Basis der Worst-Case-Simulation ergibt. Bereich II enthält die Reserven der Worst-Case-Planung, da beispielsweise die Überlagerung von Rückspeisung und Bezug vernachlässigt wird. Bereich III stellt den letzten Baustein zur maximalen Ausreizung des Spannungsbandes dar. Er entsteht, da bei der Worst Case Planung lediglich $U_{min}$ und $U_{max}$ berücksichtigt werden, aber nicht die zeitliche Korrelation. Löst man sich von diesem Ansatz, so ist die maximal auftretende Spannungsspreizung $\Delta U_{max}$ (Maximum der Differenz von $U_{max}(t)$ und $U_{min}(t)$ ) ausschlaggebend. Der entsprechende Potentialbereich liegt zwischen den durch $U_{max}$ und $U_{min}$ abgesteckten Niveaus und den beiden Spannungsniveaus $U_{max}(t)$ und $U_{min}(t)$ an $\Delta U_{max}(t)$ .

Abbildung 4: Spannungsband, offene Potentiale

In den folgenden Abschnitten werden Regelkonzepte beschrieben, die zur Erschließung dieser Spannungsbandreserven/Potentiale eingesetzt werden können. Sie stellen dabei völlig neue Ansätze dar, da nicht mehr ausschließlich das Spannungsniveau der MS-Ebene die treibende Stellgröße ist, sondern auch Zusatzinformationen der NS-Ebene eingebunden werden. Prämisse bei der Beschreibung der Regelstrategien ist, dass ein sofortiger Nutzer für die Netzplanung, d. h. ein Plus beim nutzbaren Spannungsband, ausweisbar sein muss.

Spannungsinformation NS-Ebene

Zur Bestimmung der Spannungsinformation aus der NS-Ebene wurden zwei Varianten betrachtet:

Abgesetzte Spannungssensoren,
die den Spannungswert direkt Messen und über IKT an die RONT-Regelung weiterleiten

Stromcompoundierung,
bei der über eine Strommessung an den Abgängen der ONS auf das Spannungsniveau im NS-Strang indirekt über wahrscheinlichkeitstheoretische Betrachtungen rückgeschlossen wird.

Die Standard-Sammelschienenregelung plus die Spannungsinformation aus der NS-Ebene bilden dann die Grundlage für die Regelstrategien dynamische Regelbandbreite bzw. dynamischer Sollwert.

An dieser Stelle sei angemerkt, dass mittel- bis langfristig auch Netzsimulationen zur genauen Abbildung der Spannungsverhältnisse in der NS-Ebene verwendet werden können. Eine exakte Nachbildung des Verbraucherverhaltens (Leistungsaufnahme, Gleichzeitigkeitsfaktoren, Unsymmetrien usw.) sowie die richtige Prognostizierung von Einspeisern sind hierbei zwingend erforderlich. Da derzeit die detaillierte Modellierung von NS-Netzen zu aufwändig erscheint und die benötigten Eingangsdaten zur Beschreibung der Kundenanlagen fehlen, wird dieser Ansatz nicht explizit in den nachfolgenden Abschnitten diskutiert.

Abgesetzte Spannungssensoren (ASS)

Unter abgesetzten Spannungssensoren (ASS), werden Sensoren beschrieben, die in den NS-Strängen an sensiblen/kritischen Netzknoten installiert werden und der RONT-Regelung Augenblickswerte der Spannungssituation zur Verfügung stellen (siehe Abbildung 5). Eine stabile und sichere IKT zur Datenübertragung wird bei den weiteren Betrachtungen als gegeben vorausgesetzt.

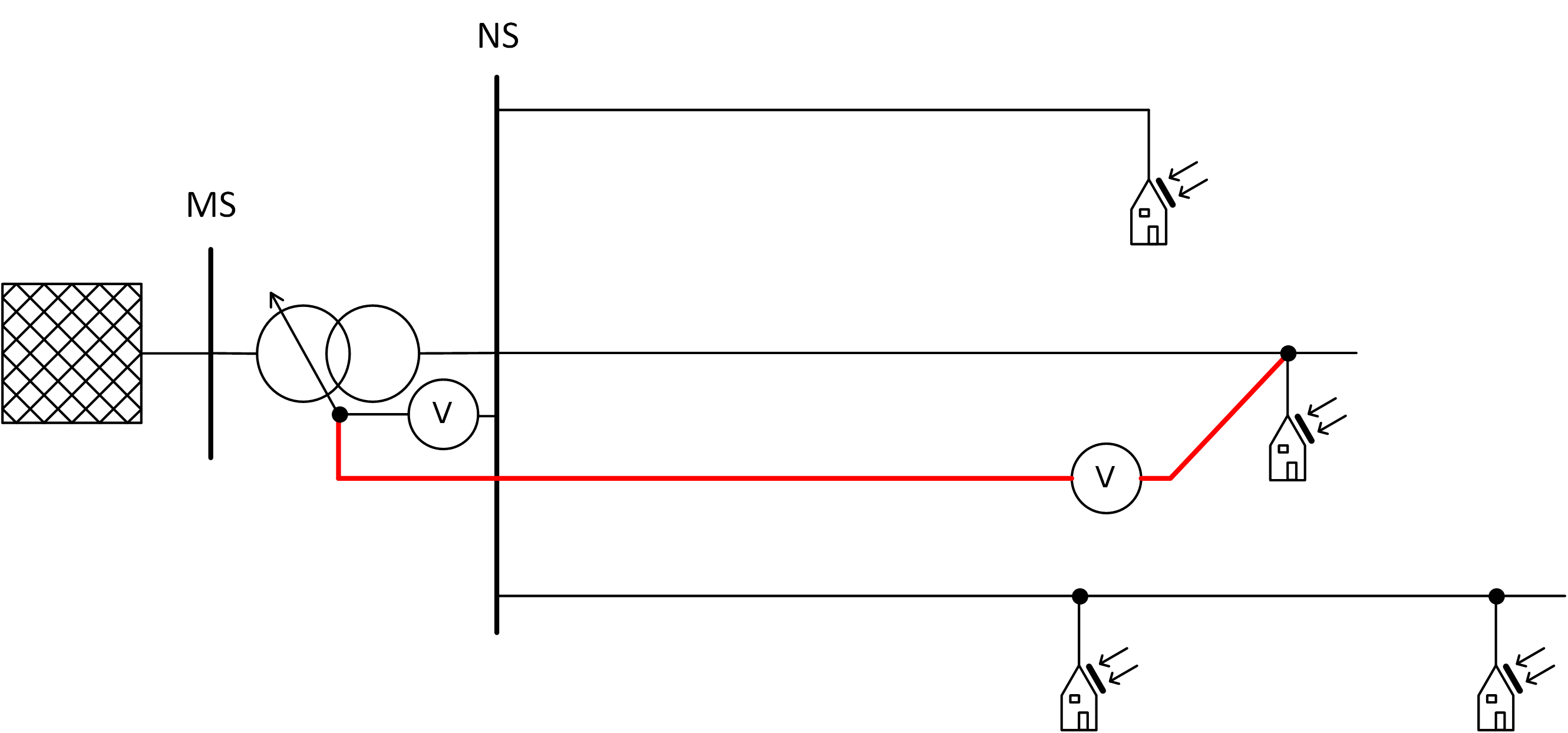
Abbildung 5: Spannungssensoren (ASS), die in den NS-Strängen an sensiblen/kritischen Netzknoten installiert werden

Entscheidend für die Zuverlässigkeit der Regelung ist die Wahl der/des kritischen Netzknoten. Hierbei sind verschiedene Ansätze denkbar:

Flächendeckende Messung

Messung von Extremknoten

Messung eines kritischen Netzknotens

Die flächendeckende Messung/Überwachung aller Netzknoten im NS-Netz bietet die größte Sicherheit, allerdings ist damit auch der größte Aufwand verbunden. Im Zuge des Smart-Meter-Rollouts könnte sich diese Variante aber langfristig etablieren.

Die Anzahl der Messpunkte kann reduziert werden, wenn man sich im nächsten Schritt vergegenwärtigt, dass die Spannungsmaxima im Einspeisefall immer am Strangende bzw. am Anschlusspunkt der letzten EZA auftreten. Im realen Netzbetrieb, bei dem Einspeisung und Verbrauch gleichzeitig auftreten, können deshalb keine höheren Spannungswerte im Netz auftreten (unsymmetrische Belastung vernachlässigt). Eine Überwachung der letzten EZA eines Stranges mit ASS würde also ausreichen.

Die letzte Möglichkeit beschreibt die Installation eines ASS am kritischen Netzknoten. Hierbei wird berücksichtigt, dass die Installation an EZA im NS-Netz nicht schlagartig geschieht sondern in diskreten Schritten. Im Zuge des Zubaus stößt der Netzbetreiber auf Basis seiner bisherigen Planungsweise (die bislang auch einen sicheren Netzbetrieb sicherstellte) an die Aufnahmekapazität seines Netzes. Ursächlich ist dann eine bestimmte EZA, die an einer genau definieren Stelle im Netz installiert wird. Nun kann über einen ASS an der letzten EZA im betroffenen Strang (muss nicht zuletzt zugebaute EZA sein) die Spannung überwacht werden. Analoges gilt für die Planung/Überwachung des Spannungsfalls im Starklastfall.

Die Wahl der zu überwachenden Netzknoten kann neben den eben vorgestellten netzplanerischen Ansätzen durch eine stochastische Auswertung von Messdaten des Netzes vorgenommen werden. Hierbei sind die auftretende Spannungsverteilung der einzelnen Knoten auszuwerten und kritische Knoten zu identifizieren. Zu beachten ist dabei die Auflösung und der Umfang der Messdatenbasis, da die Grundgesamtheit der Spannungsverteilung repräsentativ dargestellt werden muss. Beide Varianten können auch kombiniert werden, indem zunächst ASS auf Basis der 3 vorgestellten Varianten installiert werden und über eine Zusatzfunktion die aufgenommenen Messdaten archiviert und im Nachgang ausgewertet werden.

Stromcompoundierung

Bei der Stromcompoundierung oder auch lastflussabhängigen Regelung wird die Strominformation der NS-Abgänge am RONT zur erweiterten Regelung genutzt. Hardwareseitig müssen hierzu Strommesssensoren verbaut und angeschlossen werden. Der Vorteil hierbei ist, dass die Regelungseinrichtung und Sensoren örtlich nahe beieinander liegen und deshalb keine bzw. nur geringe IKT benötigt werden. Abbildung 6 zeigt die prinzipielle Anordnung im Ortsnetz.

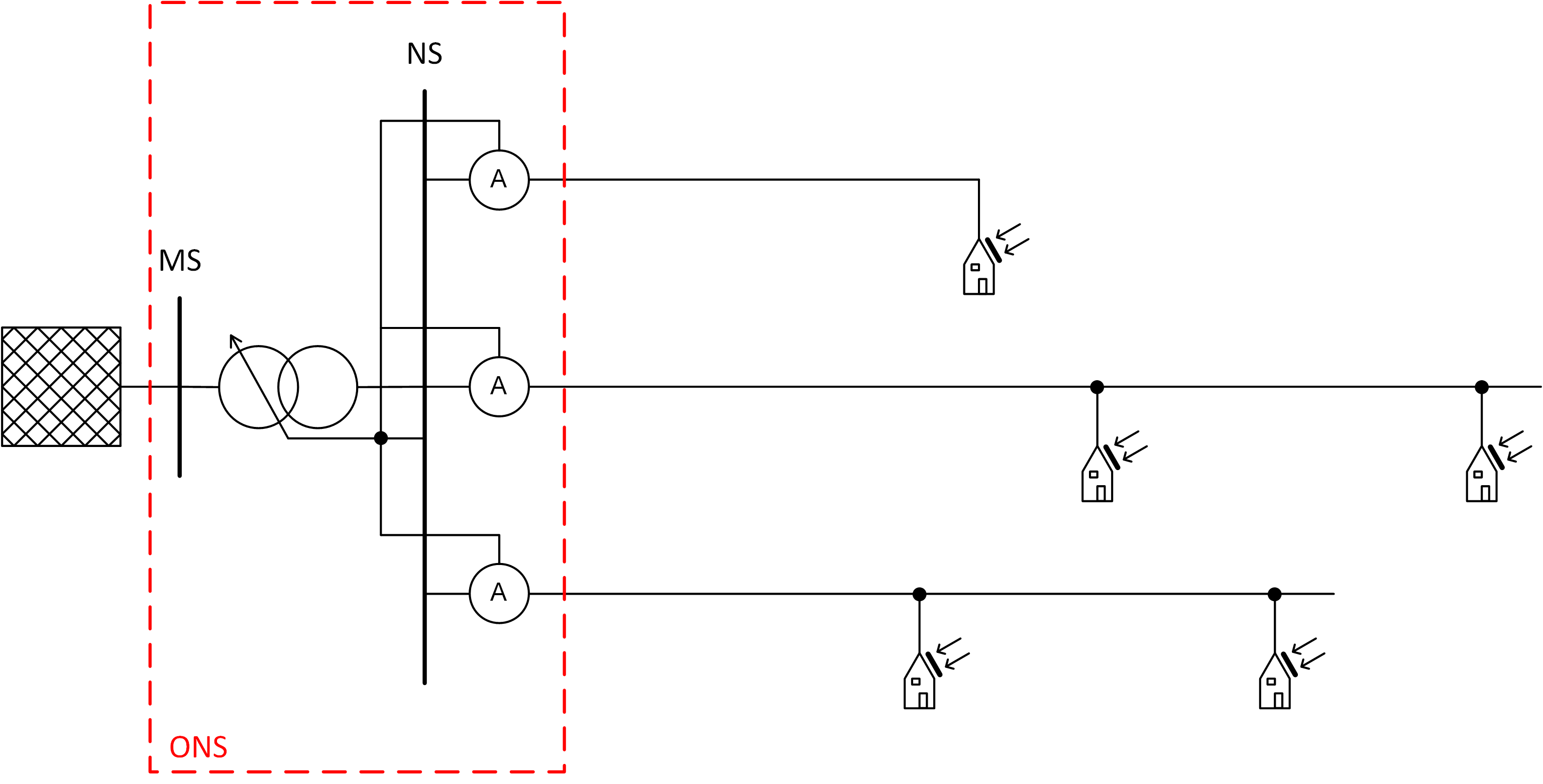
Auf die Spannungsverhältnisse im jeweiligen NS-Strang muss über die Strominformation indirekt rückgeschlossen werden. Randbedingungen hierbei sind:

die Strangtopologie (Leitungstyp, Länge, Anschlüsse),
die Verbraucher (Anzahl, Typ, Position) und
die Einspeiser (Anzahl, Typ, Position).

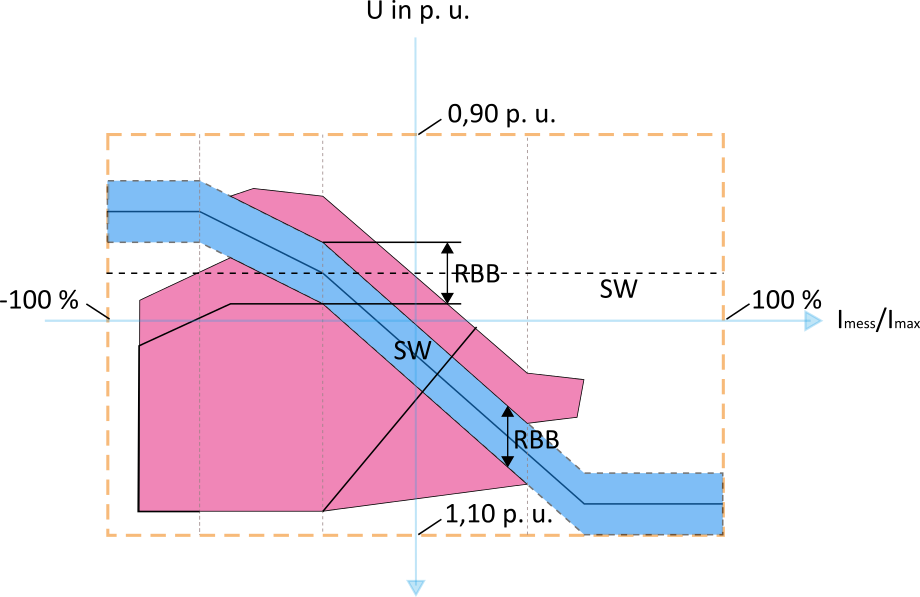
Relevant für die Stromcompoundierung ist der Spannungsfall $\Delta u$ in Abhängigkeit des gemessenen Stroms $I_{mess}$ am Abgang der Ortsnetzstation. Abbildung 7 zeigt hierzu den zulässigen Bereich (gestrichelter Rahmen). Bei einem RONT-Einsatz mit Sollwert 0,97 p.u. und Regelbandbreite ± 2 % und ausreichend großem Regelbereich ergeben sich eine zulässige Spannungsanhebung von 11 % und zulässiger Spannungsfall von 5 %. Der maximale Strom ist im Einspeise- und im Starklastfall auf den Dauerbelastungsstrom $\vert I_{E,max} \vert = \vert I_{L,max} \vert$ begrenzt.

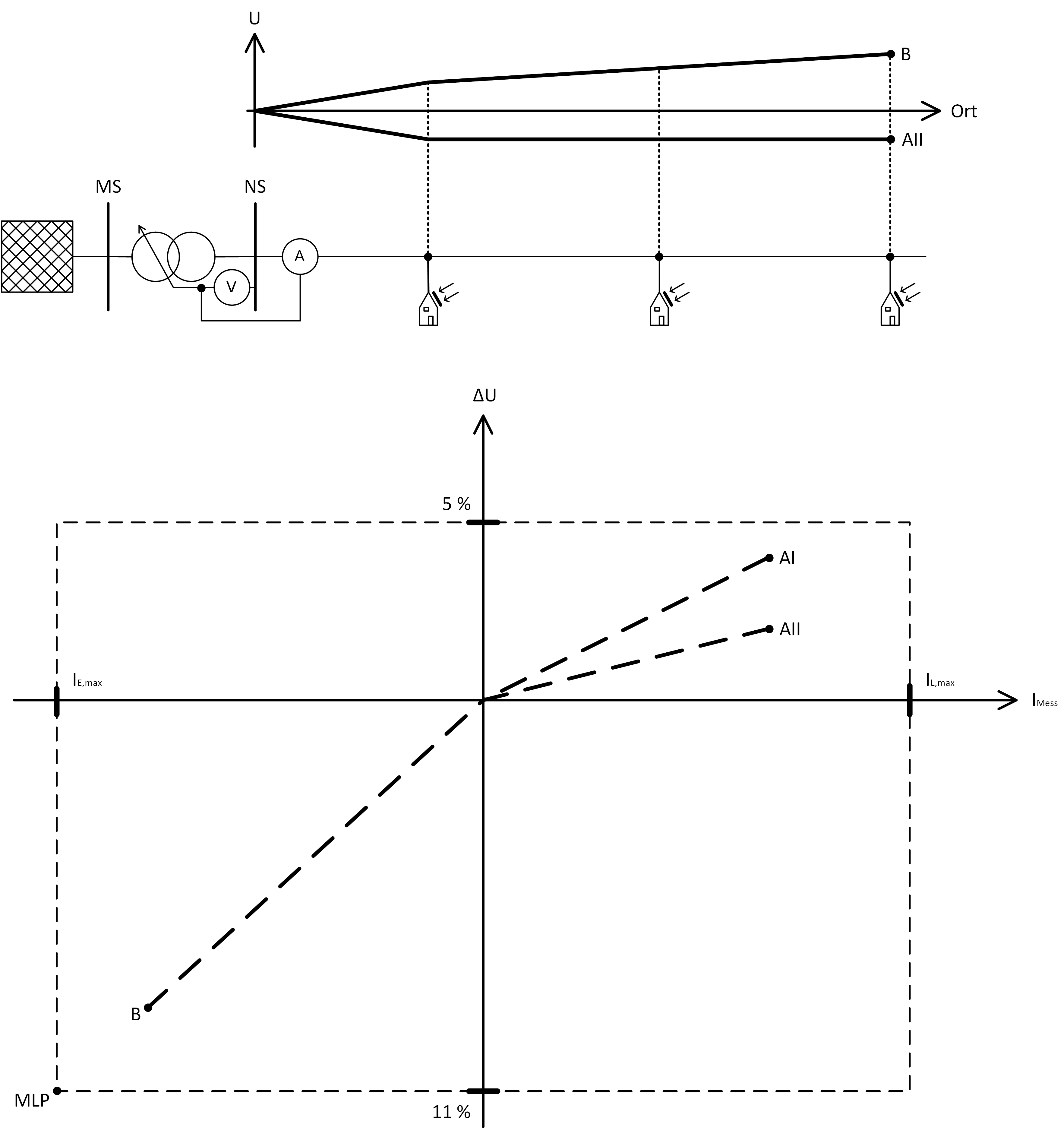
Abbildung 7: Stromcompoundierung (zulässiger Bereich)

Durch Betrachtung der Worst-Case-Szenarien (Starklast- und Einspeisefall) ergeben sich lediglich zwei Betriebspunkte an denen die Spannungsverhältnisse (Spannungsfall/-anhebung) auf den NS-Strängen in Abhängigkeit des Stroms am Abgang abgebildet werden können. Zur Abbildung des Starklastfalls wird ein Gleichzeitigkeitsfaktor [DIN 18015] herangezogen, über den die Summenlast für eine bestimmte Anzahl an Haushalten ausgewiesen werden kann. Da das Verhalten der Verbraucher nicht vorhersehbar ist, werden zwei Aufteilungsvarianten der Summenlast verwendet, wodurch sich nun drei Betriebspunkte ergeben:

Im Worst Case des Starklastfalls bezieht der Haushalt der am Strangende ist, die Maximallast für einen Haushalt und die folgenden immer die Differenz der Summenlast zur bereits vergebenen Leistung. Somit ergibt sich ein zum Strangende hin zunehmender Leistungsbezug und die maximale Spannungsanhebung (AI in Abbildung 7). Im Best Case ergibt sich die gespiegelte Aufteilung, d. h. die Leistungsaufnahme ist am Stranganfang am größten und der Spannungsfall am geringsten (AII Abbildung 7). Beide Varianten weisen nahezu den gleichen Maximalstrom auf. Unterschiede ergeben sich lediglich aufgrund der Spannungsabhängigkeit der Lasten. Die beiden Punkte geben den maximalen Spannungsfall am Strangende bzw. am letzten Verbraucher im jeweiligen Szenario an und befinden sich im 1. Quadranten.
Der Einspeisefall beschreibt den dritten Betriebspunkt, der über Punkt B in Abbildung 7 dargestellt wird. Dieser Punkt beschreibt die maximale Spannungsanhebung am Strangende bzw. an der letzten EZA und befindet sich im 3. Quadranten. Der Betriebspunkt kann durch eine Lastflusssimulation oder eine analytische Berechnung bestimmt werden.

Im nächsten Schritt muss der Übergang vom Starklastfall in den Einspeisefall und umgekehrt beschrieben werden. Einfluss auf den Verlauf hat die örtliche und leistungsmäßige Last- und EZA-Verteilung. Um nicht jeden Einzelfall separat analysieren zu müssen, wird zur Konstruktion des Verlaufs die maximal anschließbare Leistung in Abhängigkeit des Anlagenstandortes verwendet. Dies gewährleistet, dass die erzeugte Strom-Spannungsfläche, unter Verwendung eines abschnittsweisen linearen Übergangs vom Starklast- in den Einspeisfall, den reellen Übergangsverlauf inklusive einer Sicherheit abbildet. Abbildung 8 zeigt einen beispielhaften Verlauf der maximal anschließbaren Leistung in Abhängigkeit des Anschlussortes (Entfernung zur Sammelschiene). Er unterteilt sich in zwei Bereiche. Im rechten Bereich wird die anschließbare Leistung durch die maximale Auslastung, also den maximalen Strom und im linken durch die maximale Spannungsanhebung begrenzt. Dieser Zusammenhang spiegelt sich im Grenzverlauf des 3. Quadranten in Abbildung 7 wieder. Der Übergangspunkt der beiden Bereiche, der maximale Leistungspunkt (MLP), ist die links unten liegende Ecke.

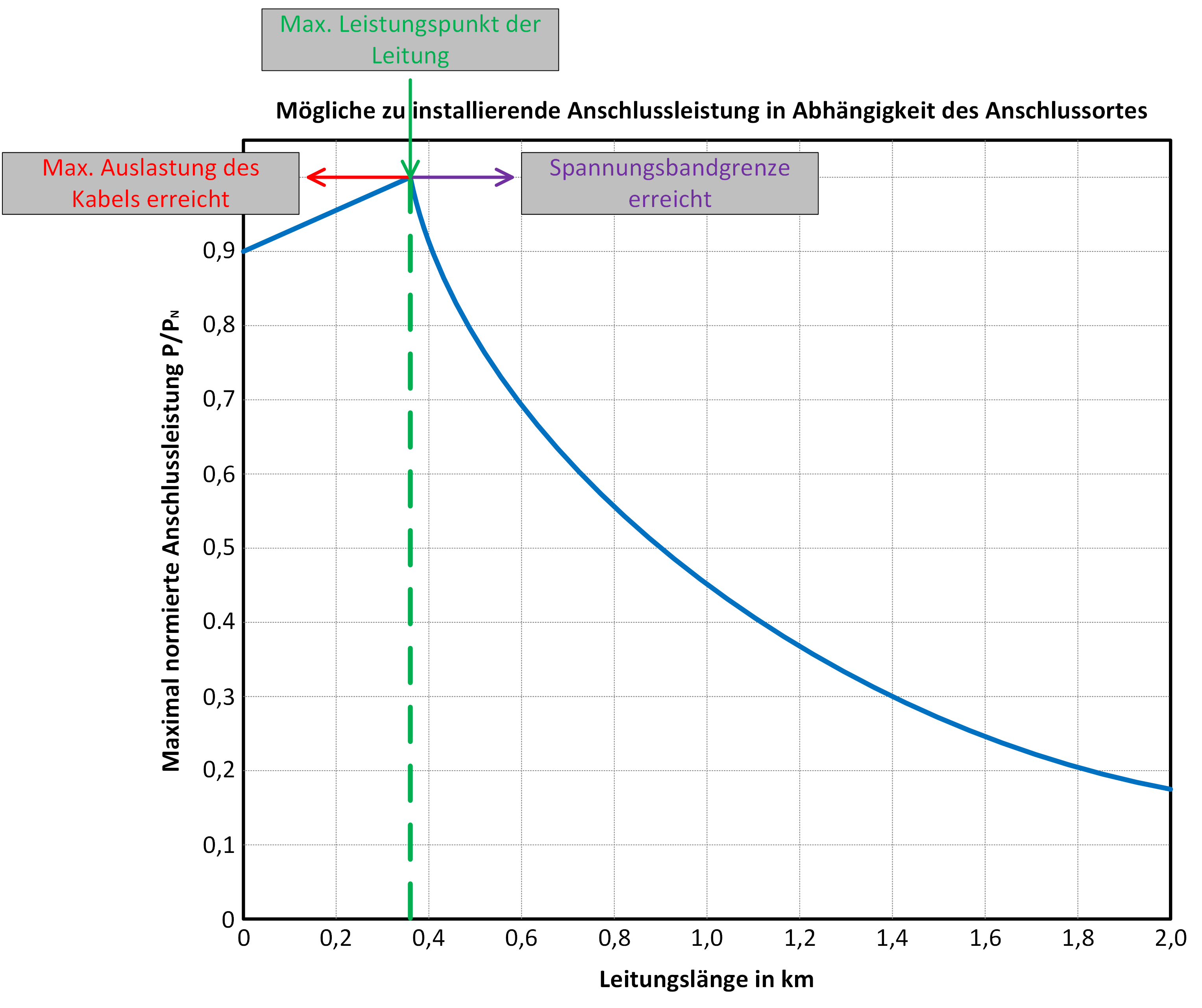
Abbildung 8: Beispielhafter Verlauf der maximal anschließbaren Leistung in Abhängigkeit des Anschlussortes (Entfernung zur Sammelschiene)

Konstruktion der Strom-Spannungsfläche:

Durch die Verwendung der maximalen Anschlussleistung am Punkt der ersten PV-Anlage (B1) und der am Strangende (B2) werden zwei Hilfskonstruktionspunkte erzeugt. Je nach Stranglänge kann B2 auf der Begrenzungslinie des maximalen Stroms oder der maximalen Spannung liegen.
Im nächsten Schritt werden die Spannungsverläufe vom Ursprung zu AI an B1 und vom Ursprung zu AII an B2 angelegt, wodurch C1 und C2 als neue Hilfspunkte entstehen.
Über die Punkt AI, C1, B1, MLP, B2, C2 und AII wird eine erste Strom-Spannungsfläche konstruiert (gelbe Fläche in Abbildung 9).
Durch Berücksichtigung des maximalen auftretenden Stroms und Spannungsanhebung am Punkt B wird die Fläche beschnitten.

Abbildung 10 zeigt hierzu ein entsprechendes Diagramm, in der die Punkte AI, C1, C1′, B, C2′ und AII die relevante Strom-Spannungsfläche aufspannen (grüne Fläche).

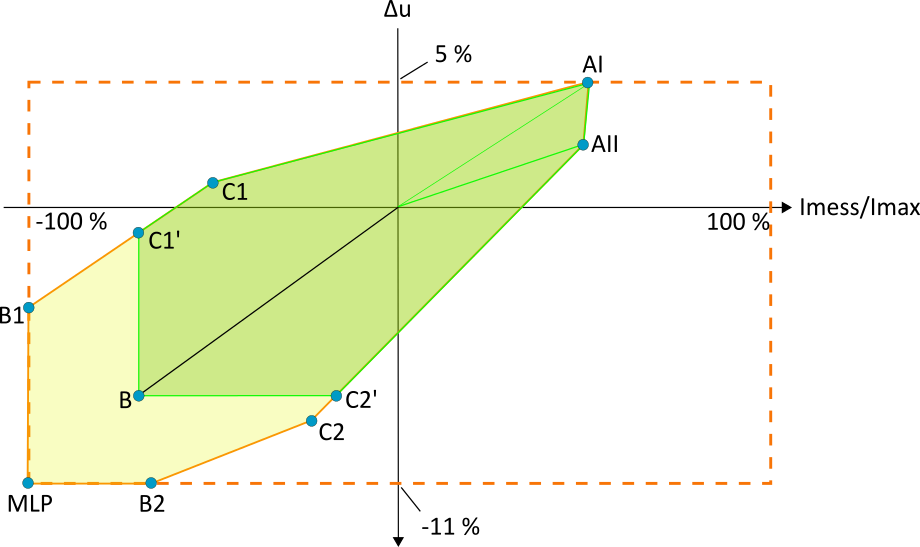
Abbildung 9: Konstruktion der Strom-Spannungsfläche

Die relevante Strom-Spannungsfläche (grüne Fläche) entsteht somit ausgehend vom Starklastfall AI durch eine lineare Anrechnung des Verlaufs der Spannungsanhebung von Punkt B1 bis zum Punkt C1. Danach erfolgt eine lineare Lastabnahme bis zum Punkt C1′. Der Verlauf über B und C2′ ist über den Einspeisefall definiert (Strom- und Spannungsextrema am Betriebspunkt B). Von C2′ aus erfolgt eine lineare Abnahme des Verlaufs der Spannungsanhebung von Punkt B2 bis AII. Durch Verbindung von AII und AI schließt sich die Fläche.

Anhand dieses Diagramms kann der zu einem Strommesswert ( $I_{mess1}$ ) zugehörige Spannungsbereich $\Delta u$ -Bereich bestimmt werden. Dieser beschreibt, welcher maximale bzw. minimale Spannungsfall im NS-Strang in Abhängigkeit der Stromaufnahme auftritt (siehe Abbildung 10).

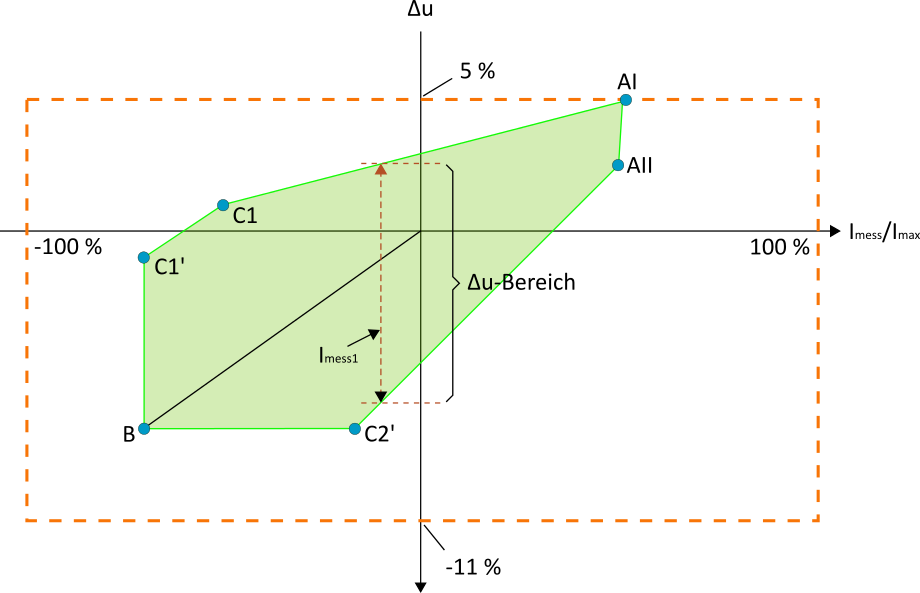
Abbildung 10: Relevante Strom-Spannungsfläche (Spannungsfall im NS-Strang in Abhängigkeit der Stromaufnahme)

Für die Qualität der Rückrechnung ist die genaue Bestimmung von Gleichzeitigkeitsfaktoren verschiedener Verbraucherkollektive (Größe und Typ) ausschlaggebend. Zusammen mit statistischen Topologieauswertungen (Stranglänge, Verbraucherabstände) wie z. B. aus [Kerber] können die Punkte AI und AII als Kennlinien vorgefertigt werden. Die Größe und Positionierung von EZA gestaltet sich sehr individuell, weshalb bei der Konstruktion des Übergangs von Starklast- in den Einspeisefall entsprechende Sicherheiten eingebaut sind. Auf eine Abbildung eines linearen Überganges mit Hilfe der Betriebspunkte AI, AII und B wird bewusst verzichtet. Wichtig ist die Berücksichtigung der Verhältnisse im Betriebspunkt B, da es sonst zu einer unnötigen Überdimensionierung des Interpretationsbereiches kommt.

Dynamische Regelbandbreite

Grundidee dieses Regelungskonzeptes ist die Erweiterung der Standard-Sammelschienenregelung um eine zeitlich begrenzte Änderung der Regelungsparametrierung.

Der Basisbetrieb wird nach wie vor durch die Standard-Sammelschienenregelung bewerkstelligt. In Betriebssituationen an denen eine Verletzung des Spannungsbandes am kritischen Netzknoten aufzutreten droht, wird anhand des NS-Spannungswertes auf Basis der ASS oder SC in die Regelung eingegriffen und die Einhaltung der Spannungsbandgrenzen sichergestellt. Bei den ASS wird dabei über die Bestimmung der/des kritische(n) Netzknoten(s) über Worst-Case-Szenarien und bei der Stromcompoundierung über WST Stochastik sichergestellt, dass kein Netzknoten im Netz einen unzulässigen Spannungswert aufweist. Der Eingriff erfolgt durch eine temporäre Verkleinerung des Regelbandes. Hierzu wird der positive Grenzwert der Regelbandbreite (d. h. die zulässige Abweichung vom Sollwert nach oben) verringert. Durch das kleinere Regelband erhöht sich automatisch das zulässige Spannungsband (siehe Abbildung 11).

Abbildung 11: Dynamische Regelbandbreite, Einfluss des Grenzwertes der Regelbandbreite

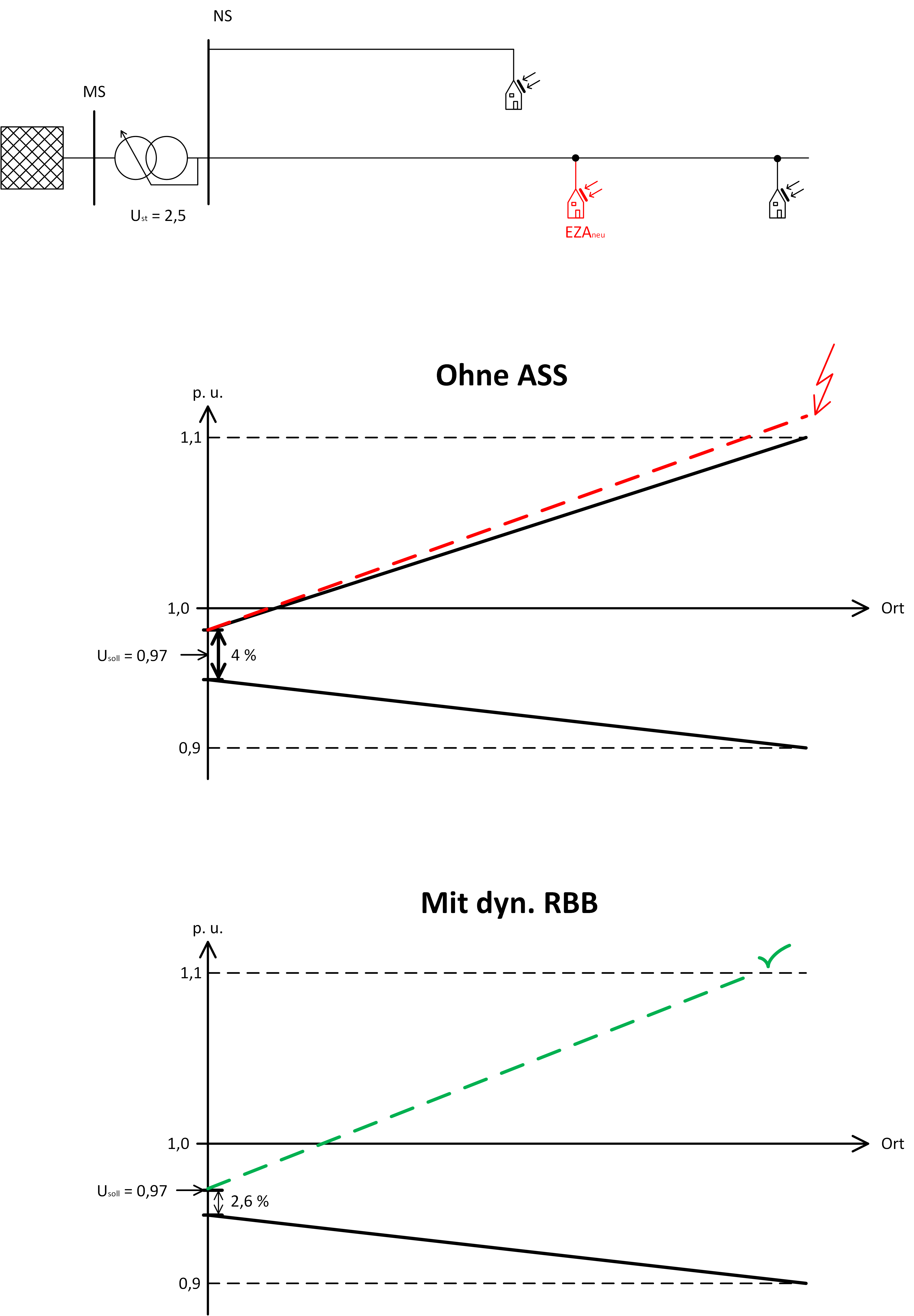
Die Verringerung des Regelbandes ist auf minimal die Breite der Stufenspannung denkbar, was allerdings ein ständiges Herab- und Hinaufstufen und damit einen hohen Kontaktverschleiß zur Folge hätte. Es wird daher empfohlen das Regelband stets etwas größer als die Stufenspannung festzulegen. Bei einer anfänglichen Regelbandbreite ( $RBB$ ) von 4 % und einer Stufenspannung ( $u_{Stufe}$ ) von 2,5 % sowie einer Reserve ( $u_{Reserve}$ ) von 0,1 % ergibt sich ein zusätzliches Spannungsband von 1,4 %, das sofort in der Netzplanung berücksichtigt werden kann. Allgemein gilt also nachfolgende Beziehung:

$u_{Zuastz} = RBB - u_{Stufe} - u_{Reserve}$

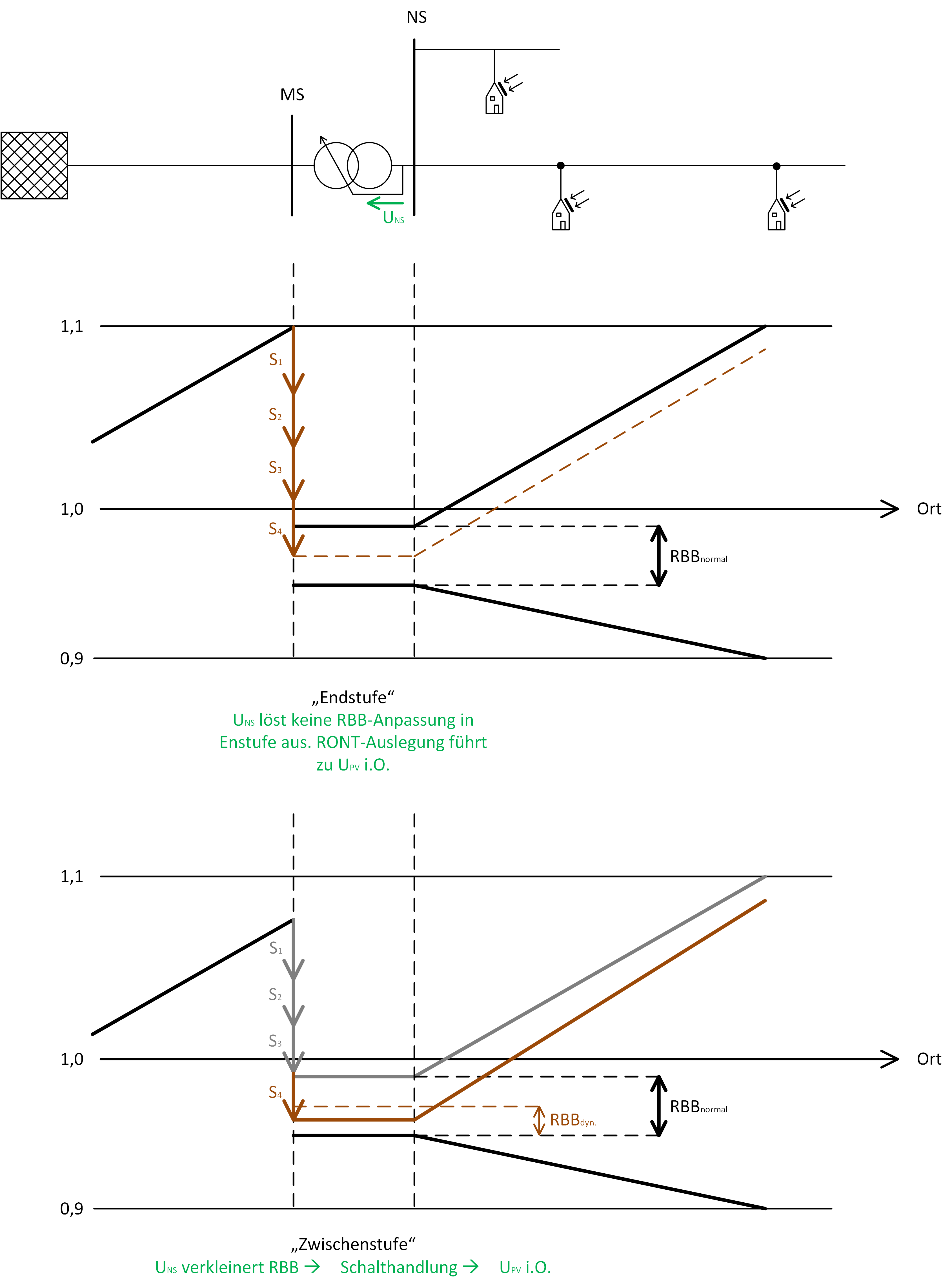
Eine dauerhafte Reduzierung der Regelbandbreite wird nicht empfohlen, da das verkleinerte Regelband höhere Schaltspiele verursacht. Bei der temporären Reduzierung hält sich dieser Effekt jedoch in Grenzen, vor allem da der Planungsansatz immer noch auf Worst-Case-Szenarien basiert und deshalb das Eintreten dieses Falles nicht zwangsläufig gegeben sein muss. Zu beachten ist, dass der Regelbereich des RONT entsprechend ausgelegt sein muss. In der Regelvariante „dynamische Regelbandbreite“ muss der RONT zum einem die Schwankung der MS-Ebene kompensieren und zudem zusätzlich eine Schalthandlung, welche von der NS-Ebene initiiert wird, zu jedem Betriebspunkt durchführen können bzw. durch die RONT-Auslegung sicherstellen, dass die Spannung an der NS-Sammelschiene in der „Endposition“ bei maximaler MS-Schwankung kleiner gleich der reduzierten Regelbandbreite ist. Abbildung 12 zeigt die Wirkungsweise der dynamischen Regelbandbreite an zwei verschiedenen Betriebszuständen. Grau eingezeichnet ist der Spannungsverlauf auf Basis der Worst-Case-Planung, der bei Betrachtung der normalen Regelbandbreite $RBB_{normal}$ zu einer Verletzung der oberen Spannungsbandgrenze führen würde. Im oberen Bild wird die Situation bei maximal positiver Schwankung der MS-Spannung gezeigt. In diesem Fall wird durch die angenommenen vier Stufen in negative Richtung (S1 bis S4) und die Höhe und Lage des Nennübersetzungsverhältnisses die maximal auftretende Spannung an der NS-Sammelschiene in der Endlage des Stufenschalters definiert (brauner Verlauf). Dieser Verlauf liegt unter dem der Worst-Case-Planung, wodurch am Strangende keine Verletzung der Spannungsbandgrenze auftritt*. Unten ist ein Betriebspunkt dargestellt, bei dem die MS-Schwankung unter den angenommen Maximum liegt und deshalb nur drei der vier verfügbaren Stufen im Einsatz sind. Im Unterschied zu den Endlagen (maximale und minimale Position des Stufenschalters) wird in den Zwischenstufen die komplette Regelbandbreite genutzt. Weshalb hier der Spannungsverlauf der Worst-Case-Planung auftreten könnte. Durch die NS-Spannungsinformation wird eine Verletzung der Spannungsbandgrenze verhindert, da eine bevorstehende Verletzung erkannt, die Regelbandbreite verringert ( $RBB_{normal}$ wird zu $RBB_{dyn}$ ) und letztendlich eine Schalthandlung initiiert wird (Stufe vier wird zugeschalten, brauner Verlauf).

* Das NS-Spannungsniveau in den RONT-Endlagen liegt trotz richtiger Auslegung nicht zwangsläufig unter den Regelbereichsgrenzen, sondern kann auch genau auf ihnen liegen. In diesem Fall würde für die Sicherstellung der korrekten Funktionsweise der dynamsichen Regelbandbreite eine zusätzliche Stufe, d. h. ein zusätzliche Wirklungs. Anzuapfunganzapfung benötigt werden. I. d. R. weist die MS-Schwankung aber deutlich kleinere Werte als ± 10 % auf, wodurch neun Stellungen bei einer Stufenspannung von 2,5 % ausreichend sind.

Abbildung 12: Wirkungsweise der dynamischen Regelbandbreite

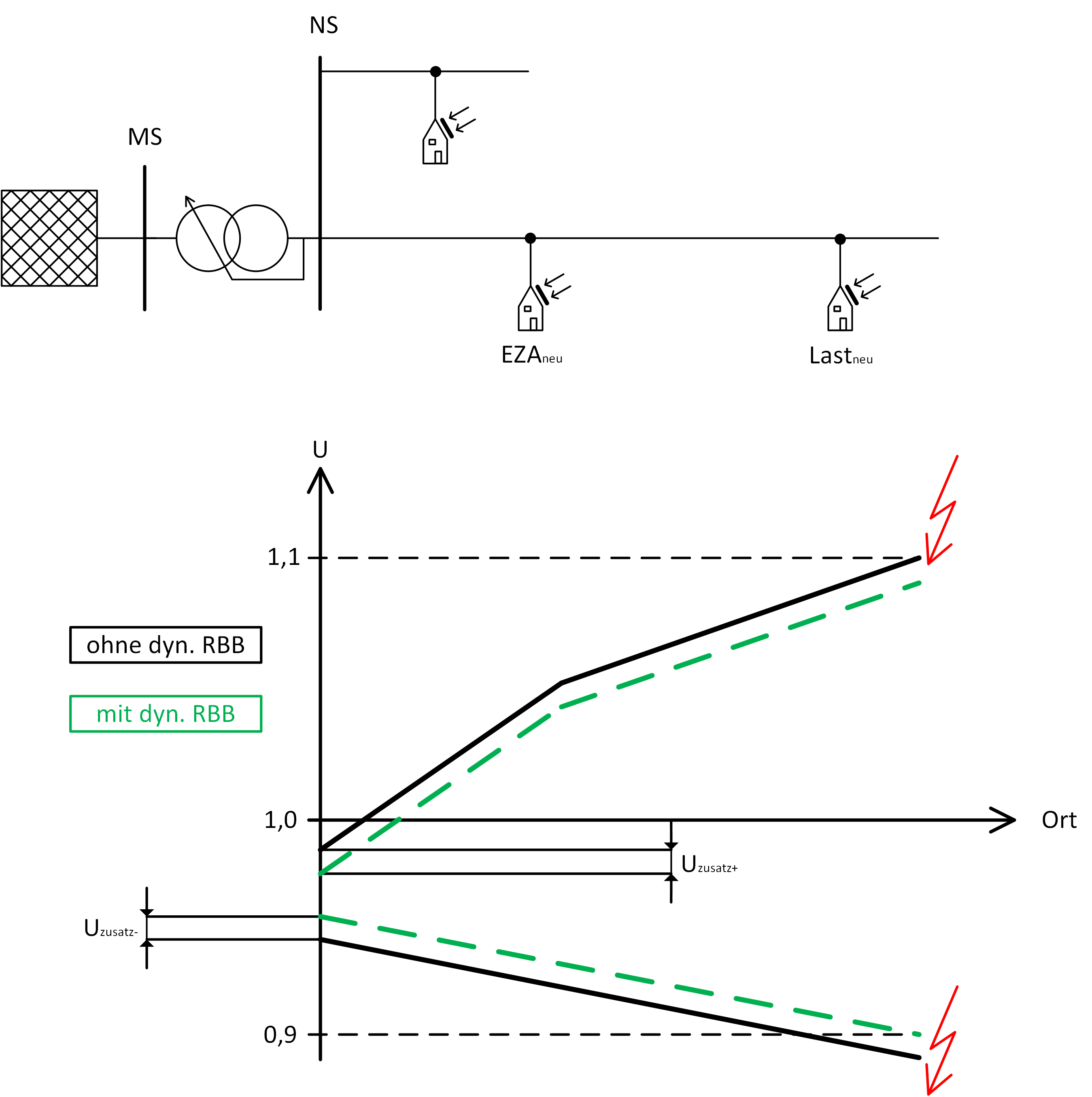
Dieses Regelungskonzept ist analog auf den Lastfall übertragbar. Auch eine parallele temporäre Reduzierung der positiven und negativen Regelbandbreite ist denkbar. Allerdings darf dabei das Regelband eine Breite der Stufenspannung zuzüglich einer Reserve nicht unterschreiten, was eine Aufteilung des zusätzlichen Spannungsbandes auf Spannungsanhebung $u_{Zusatz}+$ und Spannungsfall $u_{Zusatz}-$ voraussetzt (siehe Abbildung 13). Der Regelbereich wäre im Vergleich zur Standard-Sammelschienenregelung um eine positive und eine negative Stufe zu erweitern.

Abbildung 13: Dynamische Regelbandbreite und Aufteilung des zusätzlichen Spannungsbands

Dynamischer Sollwert

Unter der dynamischen Anpassung des Sollwertes wird eine netzzustandsabhängige Verschiebung des Spannungssollwertes und damit des Regelbandes beschrieben. Dieses Prinzip wird bereits bei der dynamischen Sollwertanpassung von Umspannwerktransformatoren eingesetzt.

In der Regel basiert die Ermittlung der Regelkennlinie auf einer vorangestellten Messreihe oder auf Erfahrungswerten des Netzbetreibers. Dies ist in der MS-Ebene durchaus praktikabel, da geringere Spannungsfluktuationen und ein homogeneres Kundenverhalten als in der NS-Ebene vorliegen.

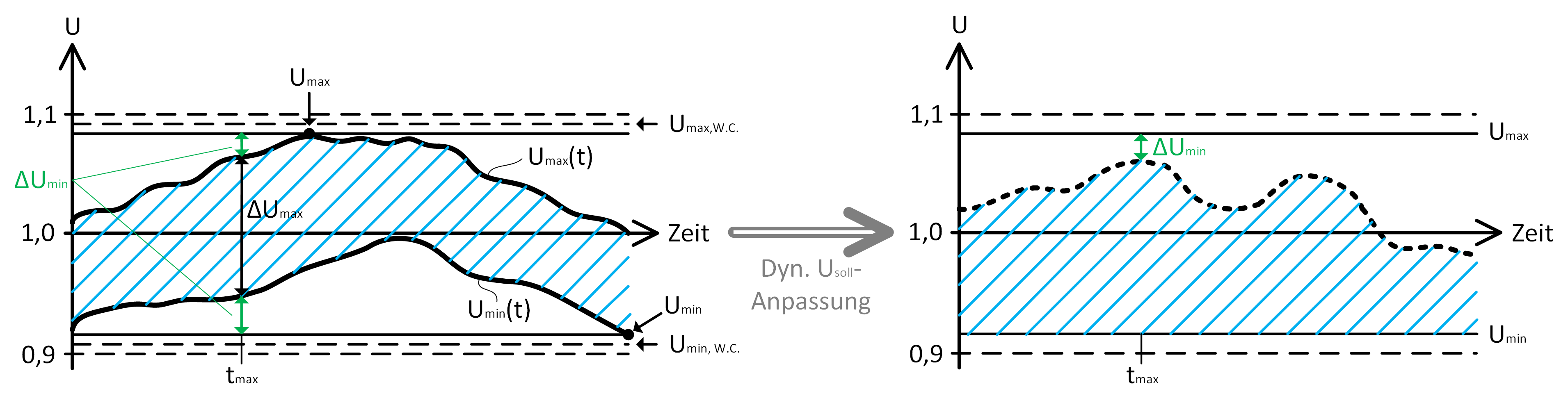
Das Grundprinzip dieses Regelansatzes besteht darin, dass nicht die Extrem-Werte $U_{max}+$ und $U_{min}+$ (siehe Abbildung 14 links) für die Auslegung von Bedeutung sind (da sie nicht zeitgleich auftreten), sondern die maximale Spannungsspreizung $\Delta U_{max}$ , welche am Zeitpunkt $t_{max}$ auftritt. Durch eine dynamische Anpassung des Spannungssollwertes kann das belegte Spannungsband (blauer Bereich zwischen $t_{max}(t)$ und $t_{min}(t)$ ) zu jedem Zeitpunkt verschoben werden. In Abbildung 14 rechts wurde der Sollwert stets so verändert, dass sich das belegte Spannungsband an die $U_{min}$ -Grenze anschmiegt und somit ein freier Bereich in Richtung $U_{max}$ entsteht. Am Zeitpunkt der maximalen Spannungsspreizung $t_{max}$ ergibt sich der minimale Abstand $\Delta U_{min}$ zur $U_{max}$ -Grenze. Dieses freie Spannungsband $\Delta U_{frei}$ ist zu jedem Zeitpunkt verfügbar und kann daher beispielsweise für den Anschluss zusätzlicher EZA genutzt werden. Diese Betrachtung lässt sich analog zur Vergrößerung des zulässigen Spannungsfalles oder bei Aufteilung von $\Delta U_{min}$ auf die gleichzeitige Vergrößerung des zulässigen Spannungsfalls und der zulässigen Spannungsanhebung durchführen. Zu beachten ist, dass für jeden vorkommenden Sollwert ein geeigneter Regelbereich des RONT zur Verfügung stehen muss.

Bei stetiger Anpassbarkeit des Sollwertes gilt:

$\Delta U_{frei} = \Delta U_{min}$ bzw. bei diskreter Anpassbarkeit:

$\Delta U_{frei} = n \cdot \Delta U_{Soll}$

wobei $\Delta U_{Soll}$ die Größe der kleinsten Sollwertänderung beschreibt und $n$ das abgerundete und ganzzahlige Verhältnis von $\Delta U_{min} / \Delta U_{Soll}$ darstellt.

Abbildung 14: Grundprinzip der dynamischen Sollwertanpassung

Entscheidend für die Wirkung der dynamischen Sollwertanpassung sind also die Verhältnisse zum Zeitpunkt $t_{max}$ , da über diese das zusätzlich nutzbare Spannungsband und somit das Plus an Anschlussleistung von EZA oder/und Lasten ausgewiesen und verplant werden kann. Um diesen Betriebspunkt zu ermitteln können einerseits Messungen (z. B. über ASS) vorgenommen oder anderseits mathematische Verfahren angewendet werden**. Bei Messungen muss sichergestellt sein, dass die kritischen Netzknoten mit erfasst werden. Zudem bedarf es einer entsprechenden Vorlaufzeit, um eine aussagekräftige/verlässliche Datenbasis zu schaffen. Deshalb wird dieser Weg im weiteren Verlauf nicht verfolgt, sondern ein analytischer Ansatz. Zur Umsetzung der priorisierten Variante müssen zwei Arbeitsschritte durchgeführt werden:

Analytische Bestimmung der Spannungsverhältnisse am auslegungsrelevanten Betriebspunkt, d. h. am Zeitpunkt der größten Spannungsspreizung $t_{max}$ , wodurch das freie Spannungsband ausgewiesen werden kann
die Beschreibung einer geeigneten Sollwertvorgabe z. B. über eine Kennlinie, damit das freie Spannungsband erschlossen wird.

** Als Ergänzung zu diesen Regelvarianten, sei die Möglichkeit einer zeitlichen Vorsteuerung erwähnt, die den Sollwert unter Berücksichtigung saisonaler Einflüsse z. B. Monatsweise vorgibt.

Bestimmung des Auslegungsfalls

Mit Hilfe der oben beschriebenen SC kann anhand eines mathematischen Modells die Spannungssituation in einem Strang in Abhängigkeit der Verbraucherstruktur und der momentanen Stromaufnahme bestimmt werden. Dieses Verfahren kann parallel auf mehrere Stränge angewendet und über die Berücksichtigung von Gleichzeitigkeitsfaktoren mehrerer Stränge zueinander die Gesamtsituation im Netz beurteilt werden. Abbildung 15 zeigt eine beispielhafte Darstellung der U-I-Fläche für drei unterschiedliche Stränge, die zusammen ein NS-Netz repräsentieren.

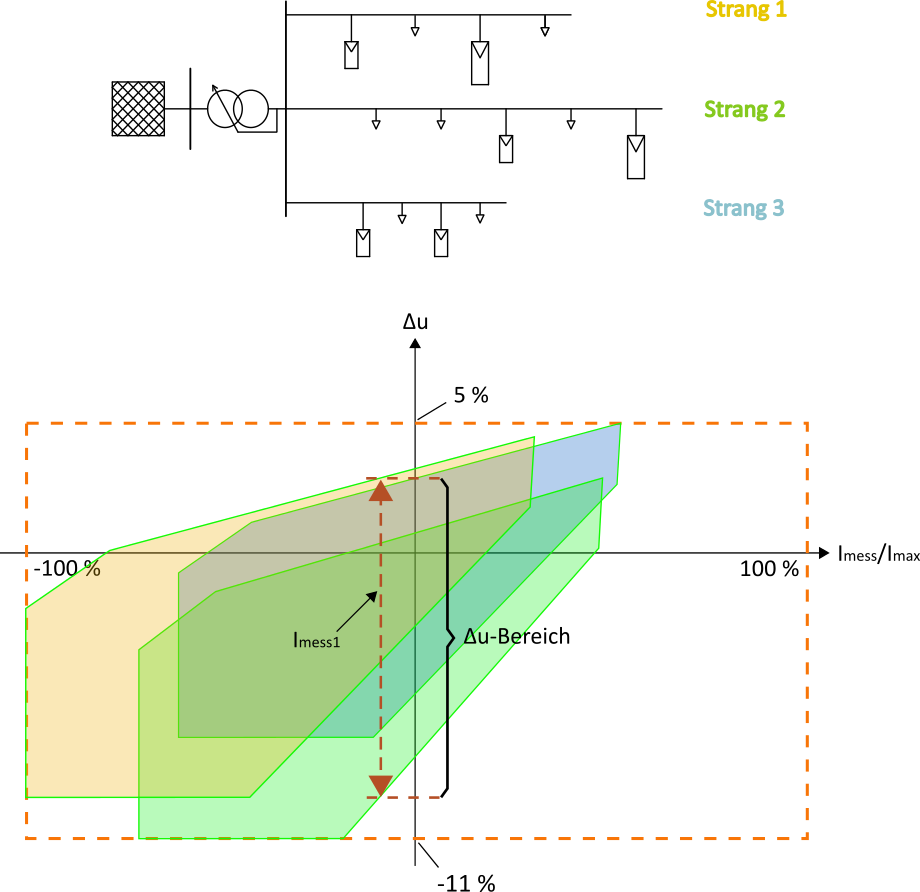
Abbildung 15: Beispielhafte Darstellung der U-I-Fläche für drei unterschiedliche Stränge

Im Hinblick auf die Gleichzeitigkeitsfaktoren gibt es zwei Extremfälle. Bei homogener Verbrauchstruktur (z. B. reine Wohnbebauung) sowie gleichmäßiger Verteilung und Ausrichtung von EZA kommt es zu einem hohen Gleichzeitigkeitsfaktor der Stränge (Abbildung 16 links), wodurch sich die relevante Strom-Spannungsfläche einfach aus der Summe aller Teilflächen konstruieren lässt und ein mögliches Potential für die dynamische Sollwertanpassung existiert. Das zweite Extremum stellt sich bei inhomogener Verbraucherstruktur sowie ungleichmäßiger Verteilung und Ausrichtung von PV-Anlagen ein (Abbildung 16 rechts). In diesem Fall können sich die einzelnen Stränge sehr unterschiedlich verhalten. Eine entsprechend hohe Spannungsspreizung zum Zeitpunkt $$t_{max}$ ist die Folge.

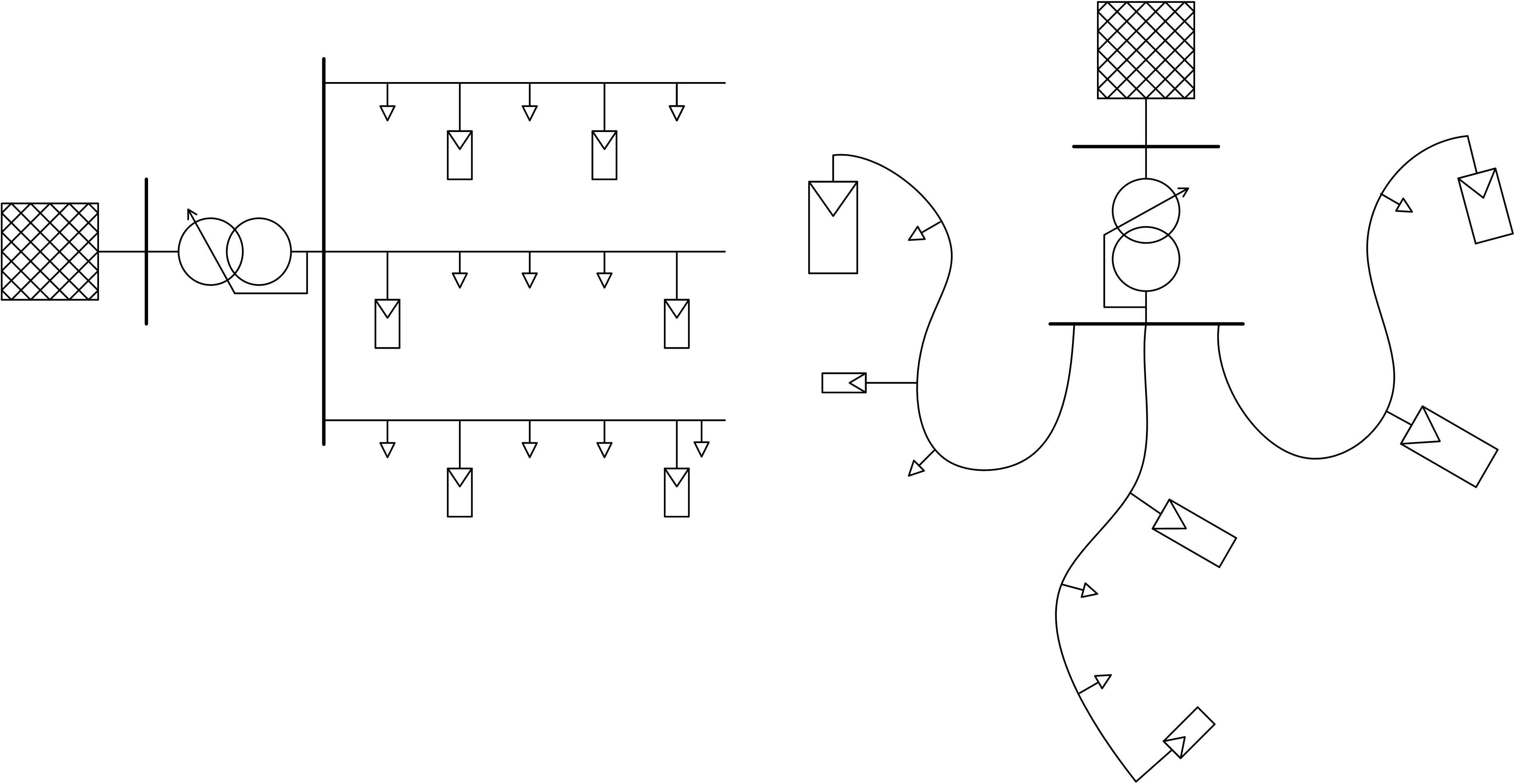
Abbildung 16: Verbrauchstruktur und Gleichzeitigkeitsfaktoren — Abbildung 16: Homogenität der Verbrauchstruktur und Gleichzeitigkeitsfaktoren

Im Extremfall eines inhomogenen Netzes muss berücksichtigt werden, dass sich die einzelnen Stränge unabhängig voneinander verhalten und somit zu jedem Zeitpunkt komplett unterschiedliche Betriebssituationen aufweisen können. Zur Konstruktion der relevanten I-U-Fläche müssen deshalb die Extrema der einzelnen Stränge kombiniert werden. Hierbei kann davon ausgegangen werden, dass mindestens ein Strang einen maximalen Spannungsfall von 5 % und ein weiterer oder auch derselbe eine maximale Spannungsanhebung von 11 % aufweist, da dieses Spannungsband bereits durch die Standard-Sammelschienenregelung erschlossen wird. Erst nach Ausreizung dieses Bereichs ist es sinnvoll durch den Einsatz der dynamischen SW-Regelung ein zusätzliches Spannungsband zu erschließen. Treten die Extrema in unterschiedlichen Strängen auf, so ergibt sich aufgrund der Unabhängigkeit der Stränge kein Potential für die dynamische Sollwertanpassung, da $U_{min}$ und $U_{max}$ laut Abbildung 17 gleichzeitig auftreten. Gibt es lediglich einen kritischen Strang, der für die Ausreizung der Spannungsgrenzen ausschlaggebend ist, so ergibt sich ein mögliches erschließbares Potential durch den Einsatz der dynamischen Sollwertanpassung.

Aus diesen Betrachtungen lässt sich zusammenfassen, dass die dynamische Sollwertanpassung

in homogenen Netzen dazu eingesetzt werden kann, um ein gleichzeitiges Spannungsproblem in mehreren Strängen oder in einem zu lösen bzw.
in inhomogenen Netzen dazu eingesetzt werden kann, um ein Spannungsproblem in einem kritischen Strang zu lösen.

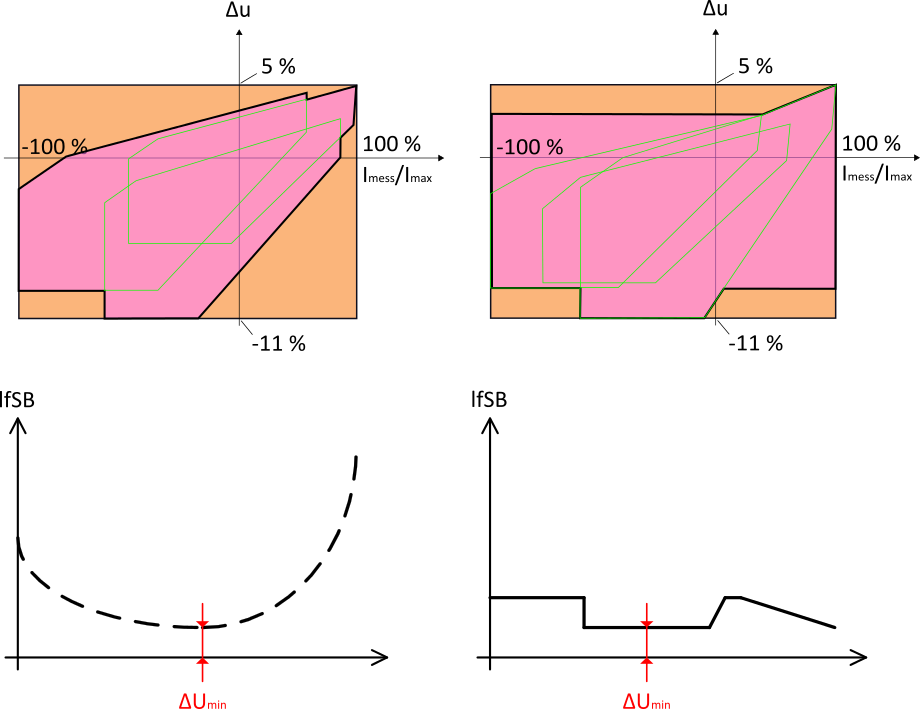
Abbildung 17 zeigt für ein homogenes Netz (oben links) und ein inhomogenes Netz mit einem kritischen Strang (oben rechts) beispielhaft die relevanten I-U-Flächen. Die Bereiche oberhalb und unterhalb der I-U-Flächen (orange Flächen) repräsentieren das freie Spannungsband in Abhängigkeit des Betriebspunktes. Die beiden unteren Diagramme zeigen das lastflussabhängige freie Spannungsband (lfSB) in einer anderen Darstellung, aus der auch der Minimalwert $\Delta U_{min}$ bestimmt werden kann. $\Delta U_{min}$ gibt an wie hoch der Spannungssollwert maximal verschoben werden kann und stellt somit das zusätzliche nutzbare Spannungsband bzw. den Spannungsbandgewinn SBG dar.

$\Delta U_{min} = SGB = min(lfSB(I_{mess}))$

Abbildung 17: Dynamische Sollwertanpassung und Extrema in unterschiedlichen Strängen

Sollwertvorgabe

Die Sollwertkennlinie wird aus der Betrachtung der I-U-Fläche abgeleitet, indem der von der Netzplanung verwendete Spannungsbandgewinn (SBG) einbezogen wird.

Im Folgenden wird von einem SBG von 2 % bei Betrachtung eines inhomogenen Netzes mit einem kritischen Strang ausgegangen. Der SBG wird hierbei für den zusätzlichen Anschluss einer EZA im kritischen Strang verwendet. Betrachtungen mit Anschluss zusätzlicher Last oder mit Aufteilung des SBG auf Lasten und EZA sind analog durchzuführen.

Ob der SBG im jeweiligen Strang genutzt werden kann hängt dabei ab wo der Betriebspunkt B (Einspeisefall) liegt. Abbildung 18 zeigt die drei möglichen Fälle. Diese sind:

B liegt innerhalb der I- und U-Grenzen im 3. Quadranten (links)
B liegt auf der I-Grenze (Mitte), unabhängig davon ob zusätzlich die U-Grenze erreicht wird oder nicht
B liegt auf der U-Grenze (rechts)

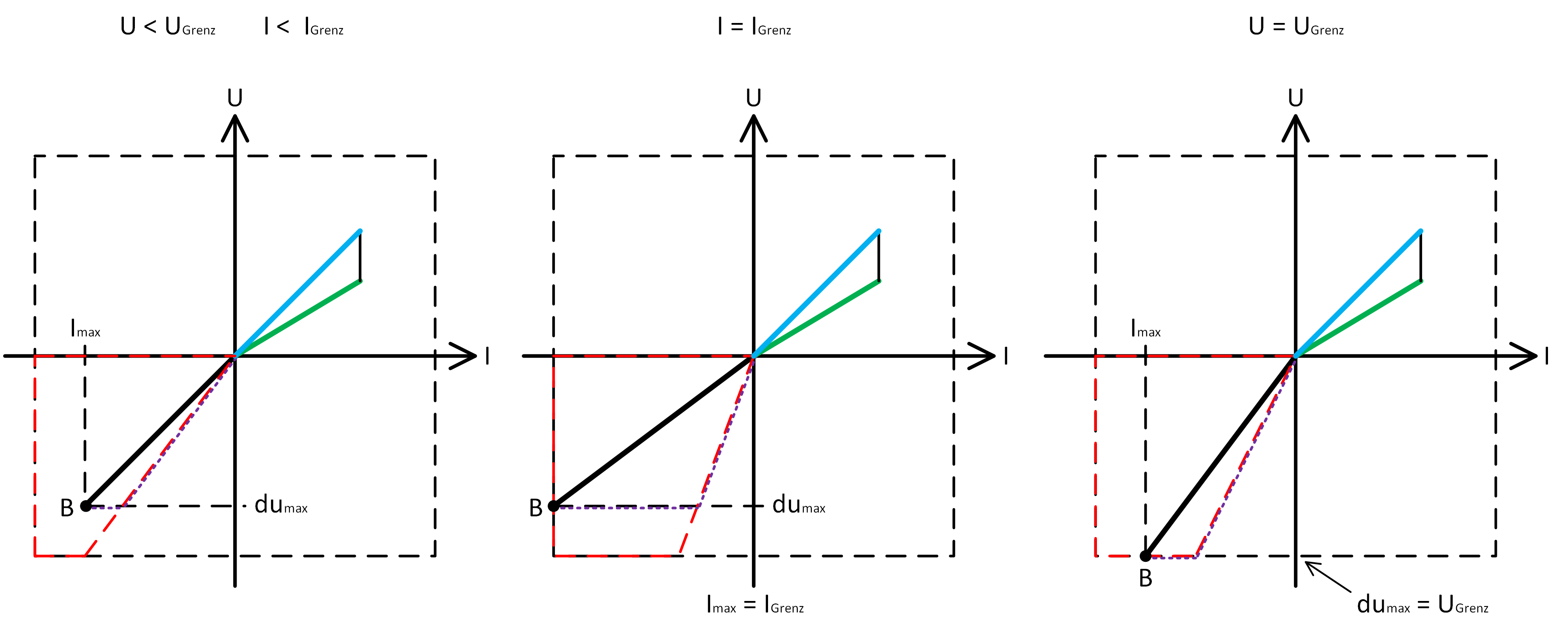
Abbildung 18: Spannungsbandgewinn (SBG), drei möglichen Fälle

In Fall 1 und 3 kann durch die Nutzung die dynamische Sollwertanpassung eine zusätzliche EZA-Leistung installiert werden, da die Spannungsanhebung das limitierende Element ist. In Fall 2 hingegen begrenzt die thermische Tragfähigkeit der Leitung den Zubau, weshalb hier kein Potential gehoben werden kann.

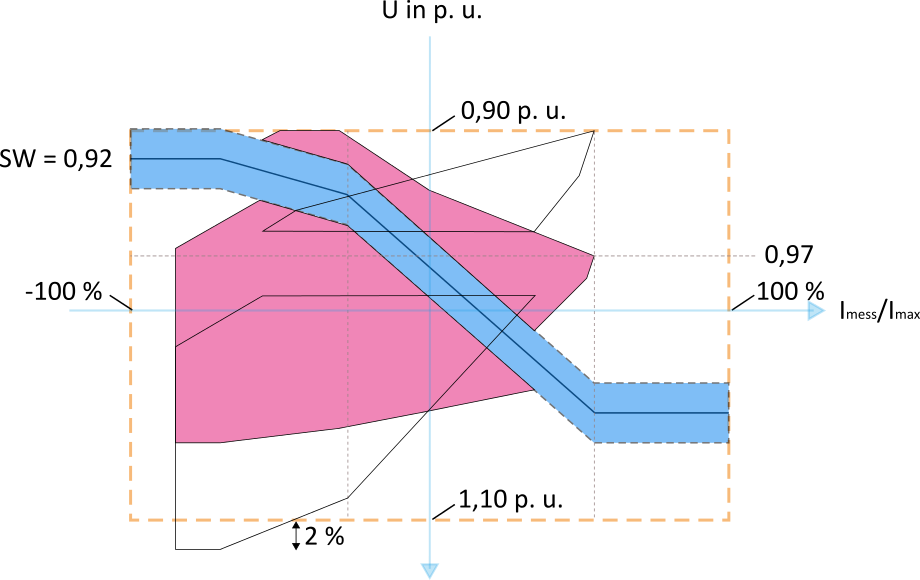
Die weiteren Planungsschritte laufen äquivalent zur obigen Konstruktionsbeschreibung. Der Unterschied zum bisherigen Vorgehen besteht in der Beschreibung der Grenzfläche. Die Stromgrenzen sind unverändert, aber die zulässige Spannungsanhebung erhöht sich um den Wert des SBG. In unserem Musterfall beträgt der SBG = 2 % wodurch sich eine maximal zulässige Spannungsanhebung von 13 % ergibt. Dies beeinflusst die maximal anschließbare Leistung und damit die Lage der Hilfskonstruktionspunkte B1 und B2. Abbildung 19 zeigt den Verlauf der maximal anschließbaren Leistung in Abhängigkeit verschiedener Spannungsgrenzwerte. Es ist ersichtlich, dass der Bereich in dem die Stromtragfähigkeit der begrenzente Faktor ist (links vom MLP) mit steigendem Grenzwert zunimmt. Dies hat zur Folge, dass der Hilfskonstruktionspunkt B2 näher am MLP liegt.

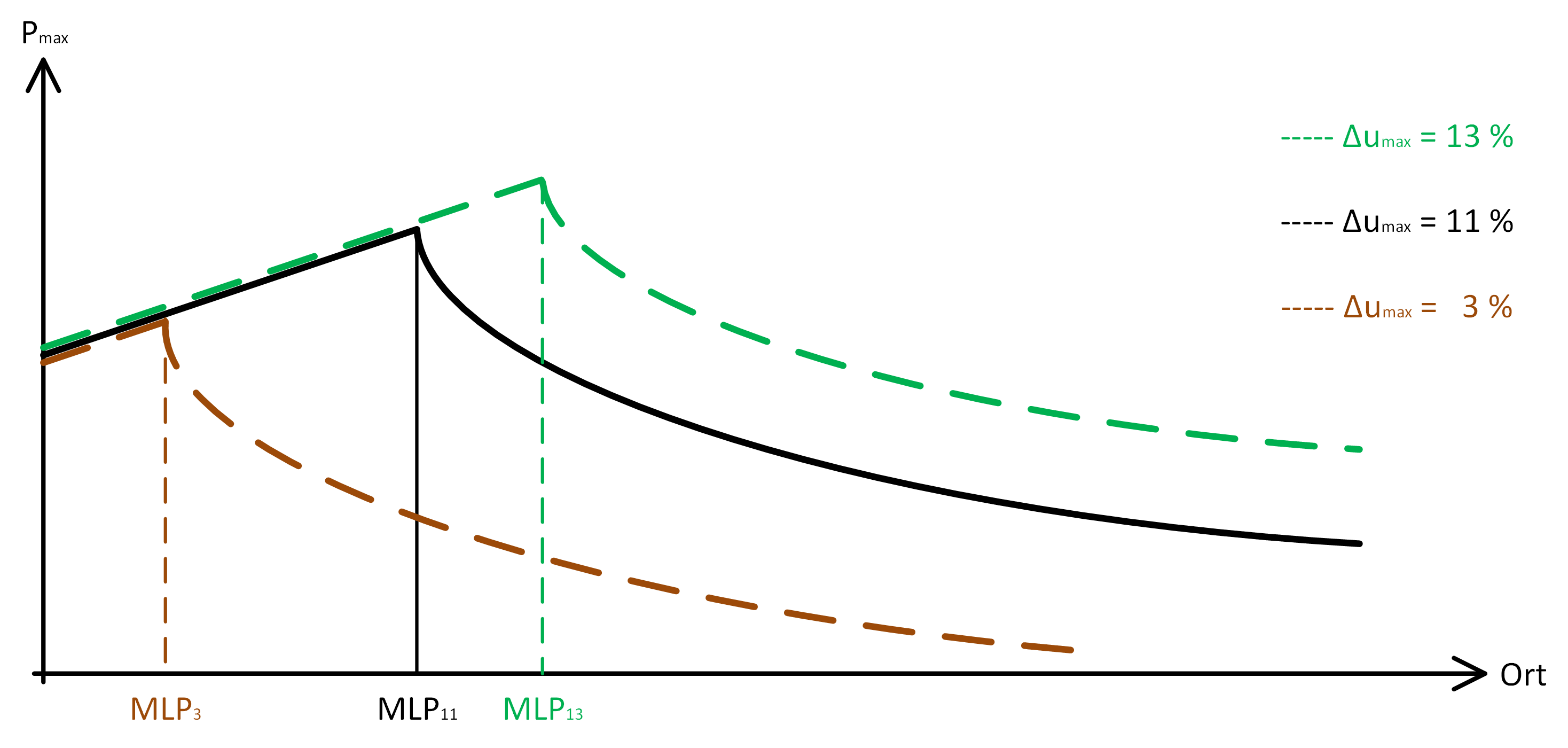
Abbildung 19: Verlauf der maximal anschließbaren Leistung in Abhängigkeit verschiedener Spannungsgrenzwerte

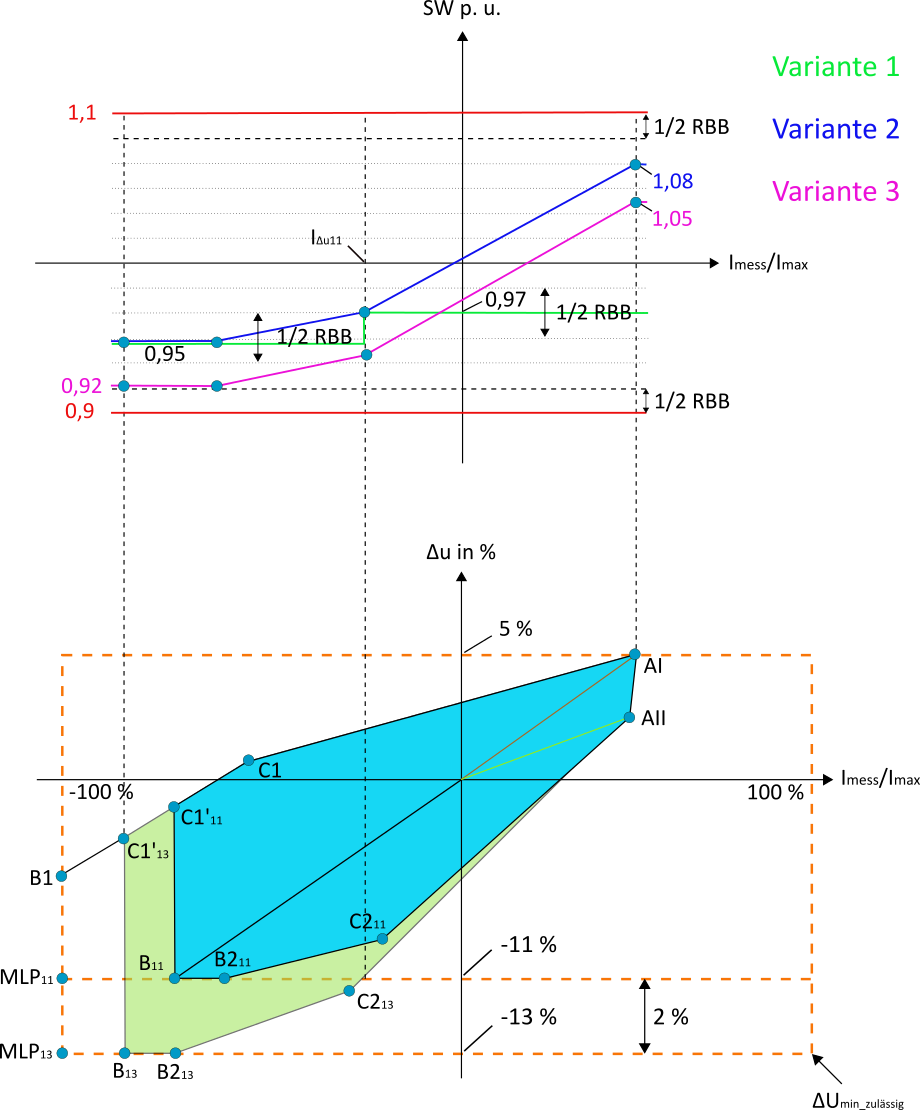
Abbildung 20 zeigt den Übergang der Strom-Spannungsfläche ausgehend von einer maximal zulässigen Anhebung von 11 % (blaue Fläche) auf 13 % (grüne Fläche). Hierbei wird davon ausgegangen, dass der Punkt B zu Beginn auf der Spannungsbandgrenze liegt und der SBG vollständig für einen zusätzlichen Zubau an EZA genutzt wird. Hierdurch wandert der Punkt B₁₁ auf den Punkt B₁₃. In Abbildung 20 (oben) werden drei verschiedene Sollwertregelkennlinien dargestellt, für deren Konstruktion allein die grüne Fläche ausschlaggebend ist:

Variante 1 (grüne Linie): Diese Kennlinie berücksichtigt, dass eine maximale Spannungsanhebung von 11 % mit dem ursprünglichen Spannungssollwert 0,97 p.u. möglich war und deshalb erst bei Überschreitung dieses Grenzwertes eine Anpassung des Sollwertes vorgenommen werden muss. Bei Überschreitung wird der Sollwert sofort um den kompletten SBG verschoben.

Variante 2 (blaue Linie): Verwendet als Bezugspunkt den Starklastfall. Ausgehend von einem maximalen Spannungsfall von 5 % bei AI wird der Sollwert auf den maximal möglichen Wert 1,08 p.u. (SW_max = 1,10 p.u. – ½ RBB) eingestellt. Anschließend wird der Verlauf der I-U-Fläche zwischen den Punkten C2₁₃ und B2₁₃ zur Konstruktion weiterer Stützstellen verwendet. An I (C2₁₃) ergibt sich der Sollwert durch Abzug der auftretenden Spannungsanhebung vom maximalen Sollwerte ( SW(C2₁₃) = SW_max – | min(∆u(C2′₁₃) | ). Im vorliegenden Beispiel ergbit sich ein Wert von 0,97 p.u. da C2′₁₃ zufällig auf der 11-%-Grenzlinie liegt. Diese Konstruktionsvorschrift ist analog auf Punkt B2′₁₃ anzuwenden. An B2′₁₃ wird die maximale Spannungsanhebung erreicht und somit das Minimum des einzustellenden Sollwertes.

Variante 3 (lila Linie): Diese Variante ähnelt sehr Variante 2, verwendet aber als Bezugspunkt die minimal zulässige Spannung (SW’_min = 0,90 p.u. + ½ RBB). Dieser Sollwert wird an der Stelle I_mess(B₁₃) angetragen. Der weitere Verlauf ergibt sich durch Betrachtung der Punkte B2₁₃, C2₁₃ und AII. Die Stützstellen ergeben sich durch Addition von SW_min mit dem Abstand des minimalen Spannungsniveaus zur maximalen Spannungsanhebung am jeweiligen Punkt ( SW(I_mess) = SW_min + – | min(∆u(I_mess) |). Beispielsweise beträgt im Beispiel der Abstand am Punkt B2₁₃ 0 p.u., weshalb sich der Sollwert auf der Linie B₁₃-B2₁₃ nicht verändert. Am Punkt C2₁₃ Beträgt der Abstand 2 p.u., weshalb sich die Stützstelle mit SW(C2₁₃) = 0,94 p.u. ergibt.

Abbildung 20: Übergang der Strom-Spannungsfläche ausgehend von einer maximal zulässigen Anhebung von 11 % (blaue Fläche) auf 13 % (grüne Fläche)

Wirkung der verschiedenen Kennlinienvarianten auf das Spannungsniveau im Ortsnetz

Zum Abschluss soll die Wirkung der verschiedenen Kennlinienvarianten auf das Spannungsniveau im Ortsnetz diskutiert werden. Hierzu verlassen wir die Darstellung des Spannungsfalls in Abhängigkeit des Stromes und betrachtet nun die Absolutwerte der Spannung (in p.u.). Hierzu ist es notwendig auch die Regelbandbreite zu berücksichtigen, welche in den folgenden Darstellungen als blaues Band gekennzeichnet ist. Um Verständnisproblemen vorzubeugen, wird die Ordinate gespiegelt und somit die steigenden Spannungswerte nach unten hin aufgetragen. Somit bleibt die Analogie zu den bisherigen Diagrammen erhalten.

Abbildung 21 zeigt die relevante Strom-Spannungsfläche ohne dynamische Anpassung des Sollwertes. Hierbei würde die obere Spannungsbandgrenze am Wert des verplanten SBG überschritten werden.

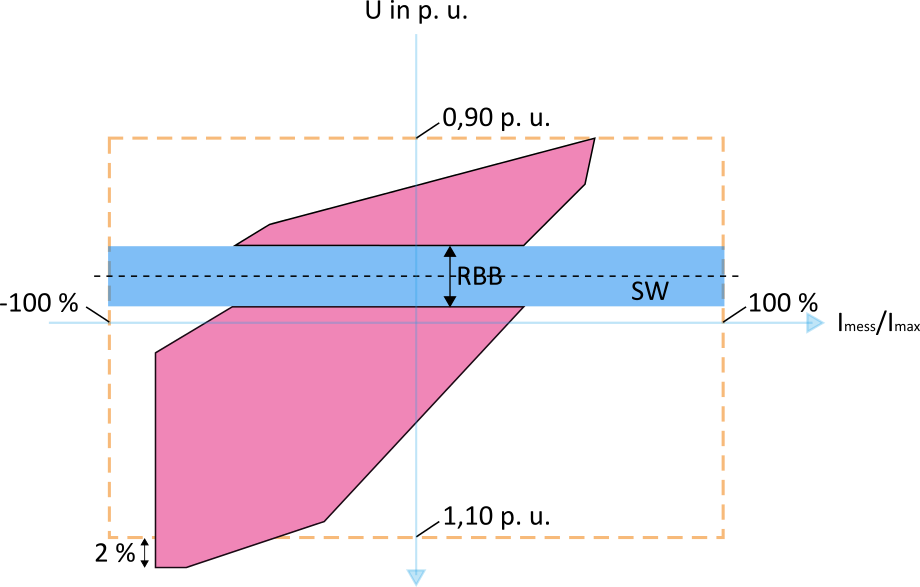
Abbildung 21: Relevante Strom-Spannungsfläche ohne dynamische Anpassung des Sollwertes

In Abbildung 22 ist nun die Strom-Spannungsfläche in Abhängigkeit einer dynamischen Sollwertanpassung nach Variante 1 dargestellt. Hierbei wird eine Überschreitung der Spannungsbandgrenze verhindert. Nachteilig bei dieser Variante ist ggf. ein zu hoher Spannungssprung, der Auswirkungen auf den Flickerpegel haben könnte. In dieser Variante sind Spannungswerte an der oberen oder unteren Grenze möglich. Wie aus Abbildung 20 und den folgenden hervorgeht ist der veranschlagte SBG von 2 % für diese fiktive Strom-Spannungsfläche zu klein gewählt, da nach der Anpassung des Sollwertes noch ein freies Spannungsband zur unteren Spannungsbandgrenze besteht. Dies spiegelt aber auch den möglichen Fall wieder, dass seitens der Netzplanung nicht der vollständige SBG verplant wurde, sondern nur ein Teil davon.

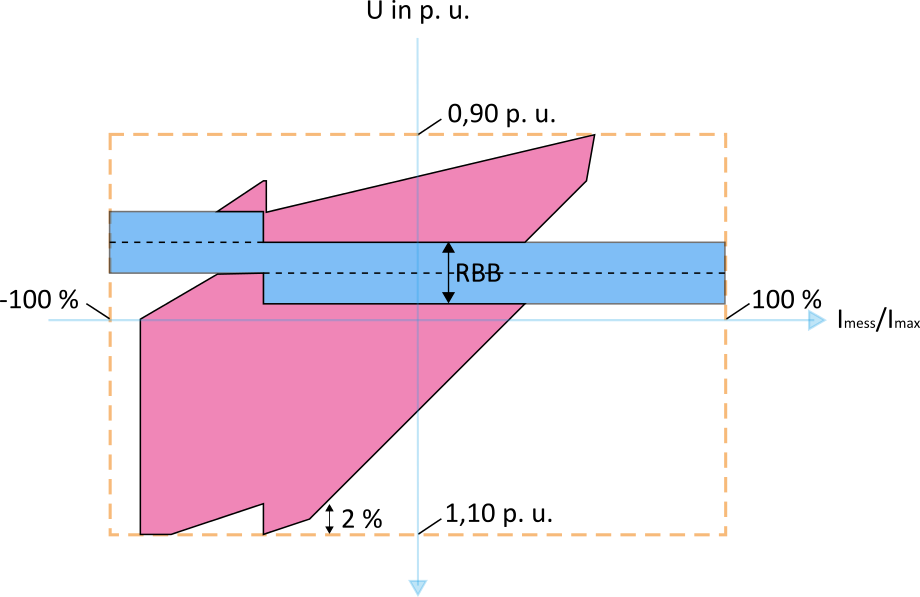
Abbildung 22: Strom-Spannungsfläche in Abhängigkeit einer dynamischen Sollwertanpassung nach Variante 1

In Abbildung 23 ist nun die Strom-Spannungsfläche in Abhängigkeit einer dynamischen Sollwertanpassung nach Variante 2 dargestellt. Hierbei wird eine Überschreitung der Spannungsbandgrenze verhindert. Da diese Kennlinie ausgehend vom Starklastfall ein möglichst hohes Sollwertniveau einstellt, ist der Abstand zur unteren Spannungsgrenze entsprechend hoch. In dieser Variante stellt sich ein hohes Spannungsniveau im Netz ein.

Abbildung 23: Strom-Spannungsfläche in Abhängigkeit einer dynamischen Sollwertanpassung nach Variante 2

In Abbildung 24 ist nun die Strom-Spannungsfläche in Abhängigkeit einer dynamischen Sollwertanpassung nach Variante 3 dargestellt. Hierbei wird eine Überschreitung der Spannungsbandgrenze verhindert. Da diese Kennlinie ausgehend vom Einspeisepunkt ein möglichst niedriges Sollwertniveau einstellt, ist der Abstand zur oberen Spannungsgrenze entsprechend hoch. In dieser Variante stellt sich ein niedriges Spannungsniveau im Netz ein.

Abbildung 24: Strom-Spannungsfläche in Abhängigkeit einer dynamischen Sollwertanpassung nach Variante 3

Hinsichtlich des RONT-Regelbereichs besitzt Variante 1 den Vorteil, dass es zwei diskrete Sollwerte gibt, für die der Regelbereich vorgehalten werden muss. Bei der Varianten 2 und 3 muss hingegen der Regelbereich jeden beliebigen Sollwert zwischen SW_min und SW_max abdecken können.

Messpunkte

Wie in den vorangegangenen Abschnitten erläutert, kann die dynamische Sollwertanpassung zur Erschließung eines zusätzlichen nutzbaren SBG in homogenen oder inhomogenen NS-Netzen mit lediglich einem kritischen Strang verwendet werden. In beiden Fällen benötigt man für die Regelung lediglich eine Messstelle.

homogenes Netz: Strommessung an einem beliebigen Abgang oder an NS-Seite RONT mit zusätzlichem Teiler
inhomogenes Netz: Strommessung am kritischen Abgang

Abbildung 25 fast die möglichen Messstellen nochmals grafisch zusammen.

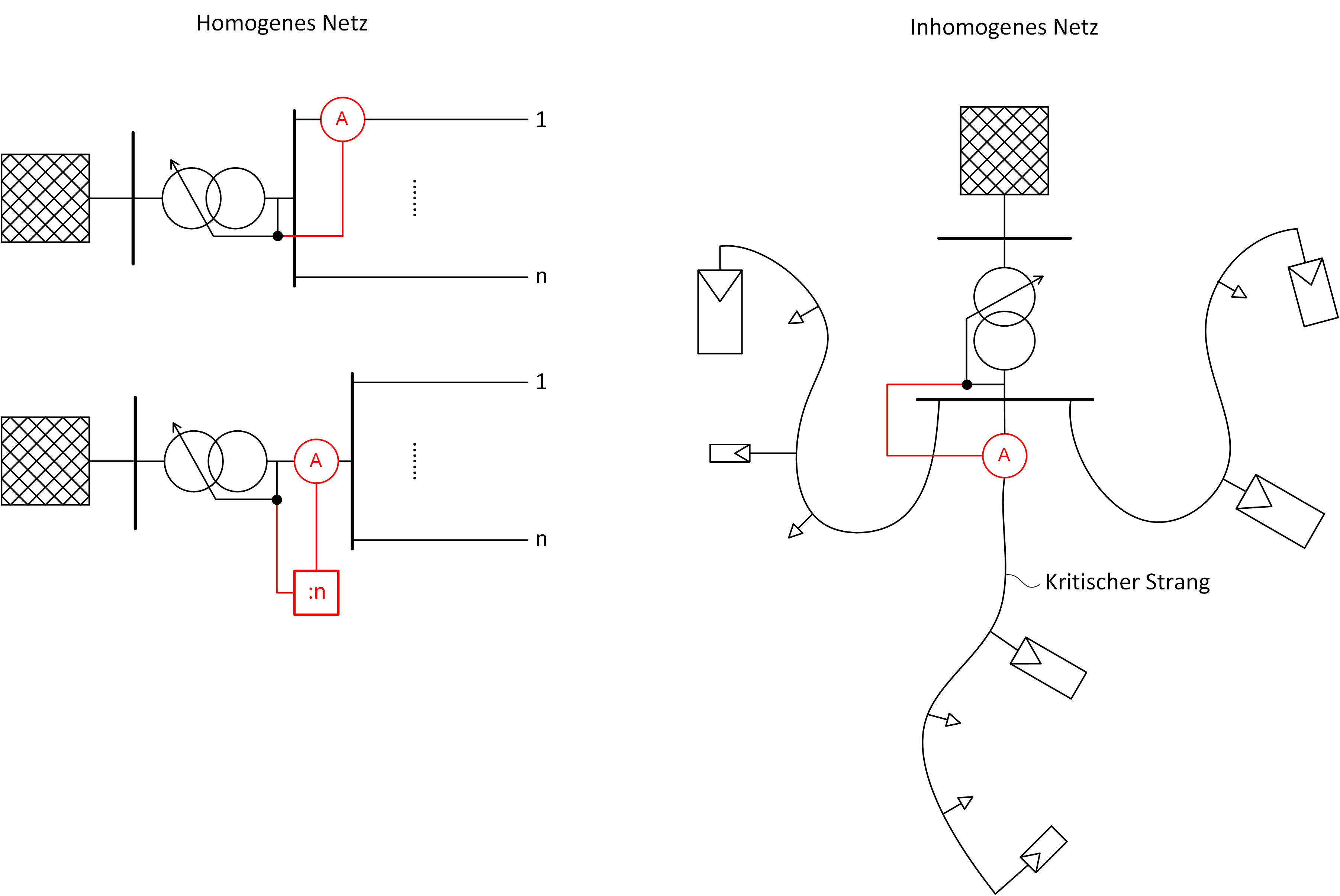
Abbildung 25: Zusammenfassung aller möglichen Messstellen

Eine NS-Seitige Messung am RONT wäre bei inhomogenen Netzen ebenfalls denkbar, jedoch wäre aufgrund der Unabhängigkeit der einzelnen Stränge die relevante Strom-Spannungsfläche mit entsprechenden Sicherheiten auszustatten, die den SBG deutlich minimieren würde. Zudem ergibt sich keine Reduzierung der Messstellenanzahl, da auch bei der Strommessung am Abgang nur der kritische Strang zu messen ist.

Übersicht Regelvarianten

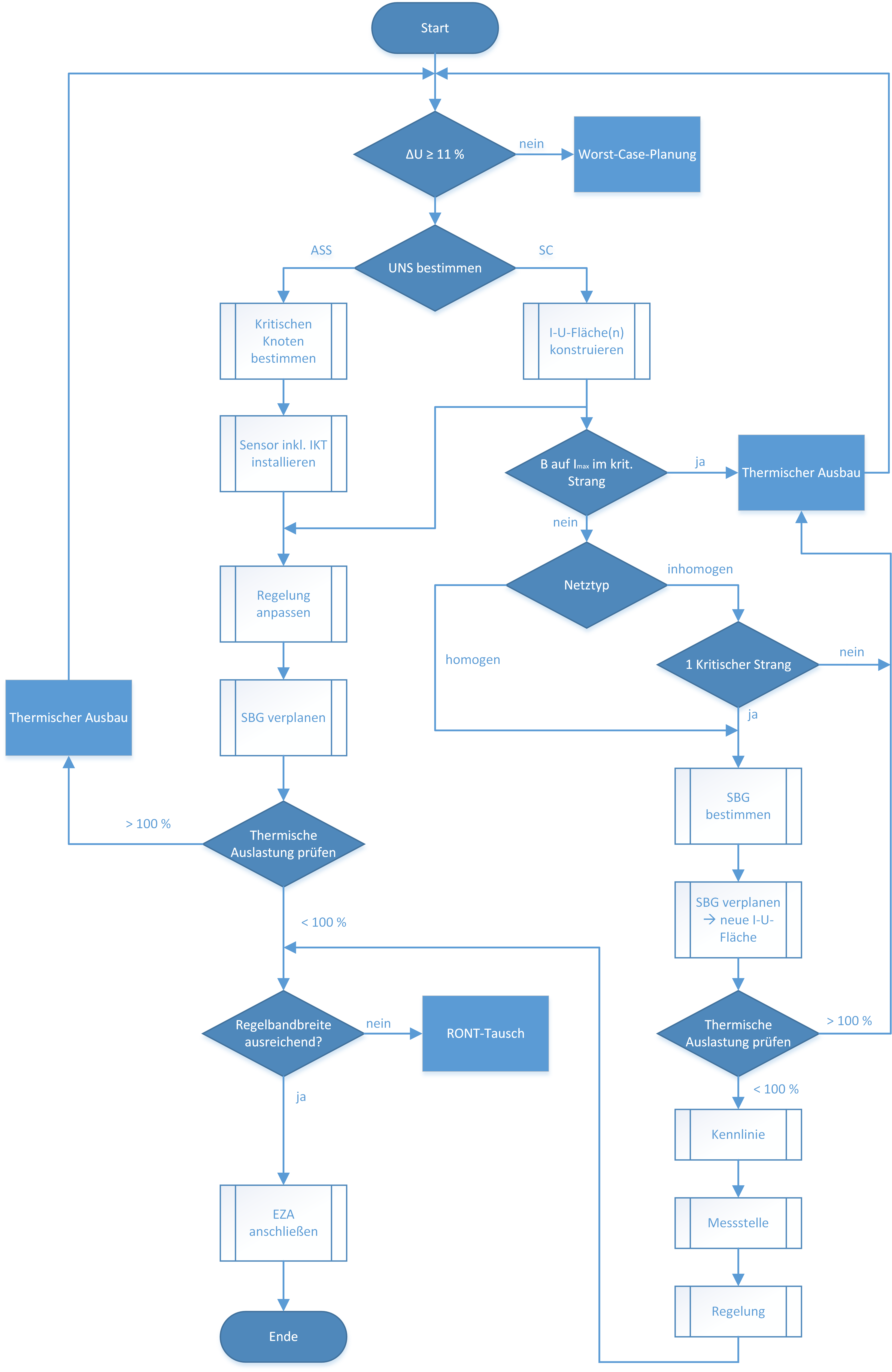
Abschließend sollen die beiden Regelvarianten dynamische Regelbandbreite und dynamischer Sollwert anhand eines Flussdiagramms, siehe Abbildung 26, zusammengefasst und die notwendigen Arbeitsschritte dargestellt werden. Der erste Verzweigungspunkt ergibt sich aufgrund der Wahl des Konzeptes zur Bestimmung der Spannungsinformation. Je nach Wahl (ASS oder SC) ist eine oder beide Regelvarianten möglich. Bei Nutzung der ASS ist nur mit Hilfe der dynamischen Sollwertanpassung ein sofortiger Spannungsbandgewinn ausweisbar. Die SC kann sowohl für die dynamische Sollwertanpassung als auch für die dynamische Regelbandbreite genutzt werden. Wichtig ist, dass immer auch die thermische Auslastung der Netzbetriebsmittel und die Regelbandbreite des RONT berücksichtig wird, da diese ggf. die zusätzlich anschließbare Leistung an Lasten und/oder EZA begrenzen.

Abbildung 26: Flussdiagramm - Regelvarianten dynamische Regelbandbreite und dynamischer Sollwert — Abbildung 26: Flussdiagramm – Regelvarianten dynamische Regelbandbreite und dynamischer Sollwert

Ausblick

Die beiden bisher diskutierten Regelvarianten basieren auf netzplanerischen Ansätzen, durch die auf das Spannungsniveau im NS-Netz rückgeschlossen wird. Die Auslegung der Standard-Sammelschienenregelung basiert dabei auf Worst-Case-Szenarien, worüber auch der kritische Punkt bestimmt wird, an dem der abgesetzte Spannungssensor (ASS) zu platzieren ist. Bei der Stromcompoundierung (SC) wird über Worst-Case-Szenarien und Gleichzeitigkeitsfaktoren die relevante Strom-Spannungsfläche konstruiert.

Mittel- bis langfristig ist ein Wandel weg von den Worst-Case-Szenarien hin zu Onlineregelungen und/oder Jahressimulationen denkbar. Die Onlineregelung setzt das Vorhandensein einer flächendeckenden Messwerterfassung (z. B. über Smart Meter) voraus. Hierdurch wäre zu jedem Zeitpunkt der Netzknoten der maximalen und der minimalen Spannung erfasst. Über Jahressimulationen, die die Netzverhältnisse mit ausreichend hoher Genauigkeit vorhersagen, wäre ebenfalls die exakte Überwachung der kritischen Knoten denkbar. In beiden Fällen könnte die Regelung auf ein fixes Regelband (Standard-Sammelschienenregelung) entfallen und Schalthandlungen nur noch bei bevorstehenden Verletzungen der Spannungsbandgrenzen eingeleitet werden. Letzteres lässt eine Reduzierung der Schaltzahlen im Vergleich zur herkömmlichen Regelung erwarten.