Für Regeltransformatoren müssen je nach Betrachtungsstandpunkt und Anordnung bzw. Eingriffspunkt der Regeleinrichtung einige Elemente im üblichen T-Ersatzschaltbild als von der Stufenschalter-Position abhängige und damit allgemein veränderliche Größen aufgefasst werden.
Für eine OS-seitige Betrachtung eines Transformators mit einer auf der OS-Seite angebrachten Regelwicklung (z. B. GRIDCON![]() ) erhält man das Ersatzschaltbild in Abbildung 1. Demnach sind selbst die Elemente der US-Wicklung veränderliche Größen, obwohl die US-Wicklung physisch unveränderlich ist. Dies erklärt sich daraus, dass die Elemente über das Übersetzungsverhältnis auf die OS-Seite umgerechnet werden und eben dieses von der Stufenschalter-Position bestimmt wird.
) erhält man das Ersatzschaltbild in Abbildung 1. Demnach sind selbst die Elemente der US-Wicklung veränderliche Größen, obwohl die US-Wicklung physisch unveränderlich ist. Dies erklärt sich daraus, dass die Elemente über das Übersetzungsverhältnis auf die OS-Seite umgerechnet werden und eben dieses von der Stufenschalter-Position bestimmt wird.
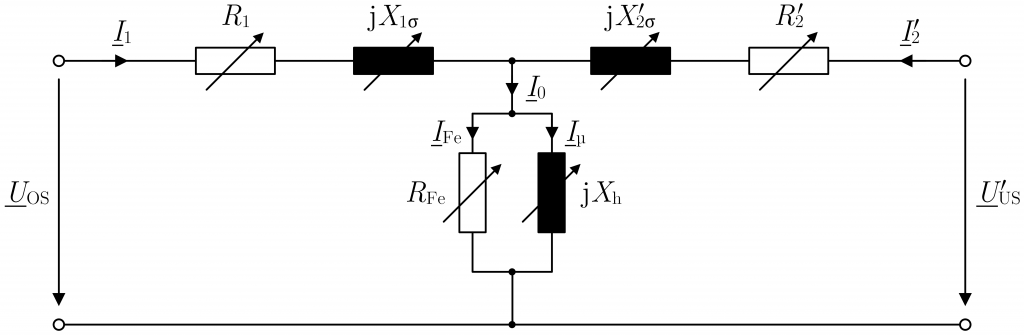
Die gezeichneten Elemente ![]() und
und ![]() repräsentieren die Kupferverluste in den Wicklungen,
repräsentieren die Kupferverluste in den Wicklungen, ![]() und
und ![]() die Streuinduktivitäten,
die Streuinduktivitäten, ![]() die Eisenverluste im Kern und
die Eisenverluste im Kern und ![]() die Hauptinduktivität.
die Hauptinduktivität.
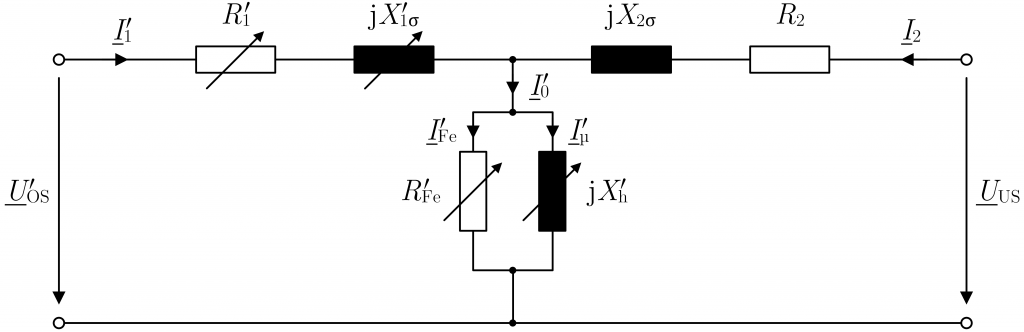
Würde man einen solchen OS-seitig geregelten RONT von der US-Seite her betrachten, so blieben der Kupferwiderstand ![]() und die Streureaktanz
und die Streureaktanz ![]() konstant, siehe Abbildung 2.
konstant, siehe Abbildung 2.
Relevante Normen zur Berechnung der Ersatzschaltbild-Elemente
Zur Modellierung von RONT sind einige relevante Normen zu beachten. Darin sind u. a. die Kurzschlussverluste ![]() und Leerlaufverluste
und Leerlaufverluste ![]() in Abhängigkeit von der Bemessungsleistung, Verlustklasse und Kurzschlussimpedanz festgelegt [1]. Laut Norm DIN EN 60076 gibt es verschiedene Kategorien für die Änderung der Anzapfungsspannung [2]. Häufig wird bei RONT die Einstellung CFVV (Constant Flux Voltage Variation) mit konstantem Fluss verwendet. Dabei sieht eine Seite des Transformators eine eingeprägte, härtere Spannung, d. h. geregelt wird die andere, weichere Spannung. Bei Ortsnetztransformatoren ist die Mittelspannung (MS) die härtere und die Niederspannung (NS), welche über das Übersetzungsverhältnis ü eingestellt wird, die weichere Spannung. Somit muss beim GRIDCON
in Abhängigkeit von der Bemessungsleistung, Verlustklasse und Kurzschlussimpedanz festgelegt [1]. Laut Norm DIN EN 60076 gibt es verschiedene Kategorien für die Änderung der Anzapfungsspannung [2]. Häufig wird bei RONT die Einstellung CFVV (Constant Flux Voltage Variation) mit konstantem Fluss verwendet. Dabei sieht eine Seite des Transformators eine eingeprägte, härtere Spannung, d. h. geregelt wird die andere, weichere Spannung. Bei Ortsnetztransformatoren ist die Mittelspannung (MS) die härtere und die Niederspannung (NS), welche über das Übersetzungsverhältnis ü eingestellt wird, die weichere Spannung. Somit muss beim GRIDCON![]() auf die OS-Seite geregelt werden, weil dann bei Abweichungen der Oberspannung weiterhin eine theoretisch konstante Unterspannung anliegt, welche in der Realität aufgrund der begrenzten, in diskreten Schritten wählbaren Anzahl an möglichen Stufenschalter-Positionen innerhalb einer festgelegten Regelbandbreite pendelt.
auf die OS-Seite geregelt werden, weil dann bei Abweichungen der Oberspannung weiterhin eine theoretisch konstante Unterspannung anliegt, welche in der Realität aufgrund der begrenzten, in diskreten Schritten wählbaren Anzahl an möglichen Stufenschalter-Positionen innerhalb einer festgelegten Regelbandbreite pendelt.
In Norm DIN EN 60076 ist außerdem beschrieben, dass sich die Nenngrößen eines Transformators auf die neutrale Stellung beziehen, welche vom Hersteller festgelegt werden muss. Dabei handelt es sich meistens um die mittlere Anzapfung [2]. Für die Berechnungen wird der Nennstrom ![]() somit in der neutralen Position für die Nennspannung
somit in der neutralen Position für die Nennspannung ![]() und die Nennscheinleistung
und die Nennscheinleistung ![]() ausgelegt, siehe Tabelle 1.
ausgelegt, siehe Tabelle 1.
TABELLE 1: BELASTBARKEIT IN ABHÄNGIGKEIT VON DEN RONT-ANZAPFUNGEN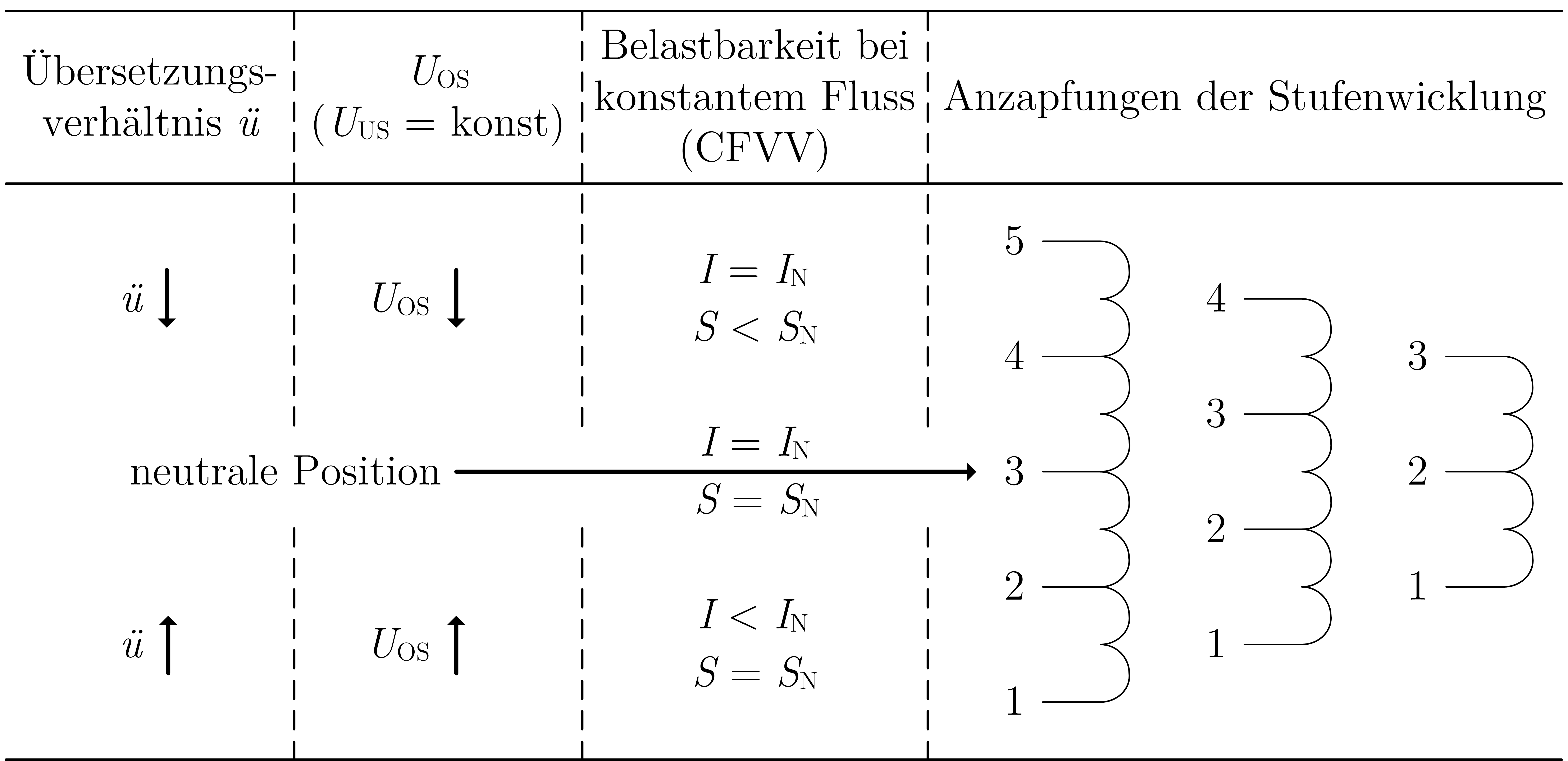
Für OS-seitig kleinere Windungszahlen ![]() wird das Übersetzungsverhältnis ü bei einer konstanten US-seitigen Windungszahl
wird das Übersetzungsverhältnis ü bei einer konstanten US-seitigen Windungszahl ![]() nach Gleichung
nach Gleichung
(1) ![]()
niedriger. Die angegebene Näherung gilt unter Vernachlässigung der vom Leerlaufstrom verursachten Spannungsänderung, da sich deren Einfluss im Allgemeinen kaum auswirkt [3]. Folglich kann die Unterspannung bei einer kleineren Oberspannung konstant gehalten werden, wobei der OS-seitige Strom den Nennstrom ![]() nicht überschreiten darf. Die übertragbare Scheinleistung ist deshalb in diesem Bereich kleiner als die Nennscheinleistung
nicht überschreiten darf. Die übertragbare Scheinleistung ist deshalb in diesem Bereich kleiner als die Nennscheinleistung ![]() des Transformators.
des Transformators.
Größere Oberspannungen können auf eine konstante Unterspannung transformiert werden, indem ein höheres Übersetzungsverhältnis durch OS-seitig größere Windungszahlen aufgeschaltet wird. Die Scheinleistung darf maximal den Wert von ![]() erreichen, weshalb der OS-seitige Strom in diesem Bereich auf kleinere Werte als
erreichen, weshalb der OS-seitige Strom in diesem Bereich auf kleinere Werte als ![]() begrenzt ist.
begrenzt ist.
Berechnungshinweise
Im folgenden Abschnitt sind Hinweise zur Berechnung der Ersatzschaltbild-Elemente von regelbaren Transformatoren zusammengefasst. Dabei gibt es Unterschiede zwischen der neutralen Stellung und den sonstigen Positionen des Stufenschalters.
Neutrale Position
Alle Widerstände und Reaktanzen beziehen sich auf das einphasige Ersatzschaltbild in Sternschaltung für einen OS-seitig geregelten RONT bei OS-seitiger Betrachtung [4], siehe Abbildung 1. Dabei werden für die Kupferverluste und Streuinduktivitäten des Transformators die Näherungen
(2) ![]()
und
(3) ![]()
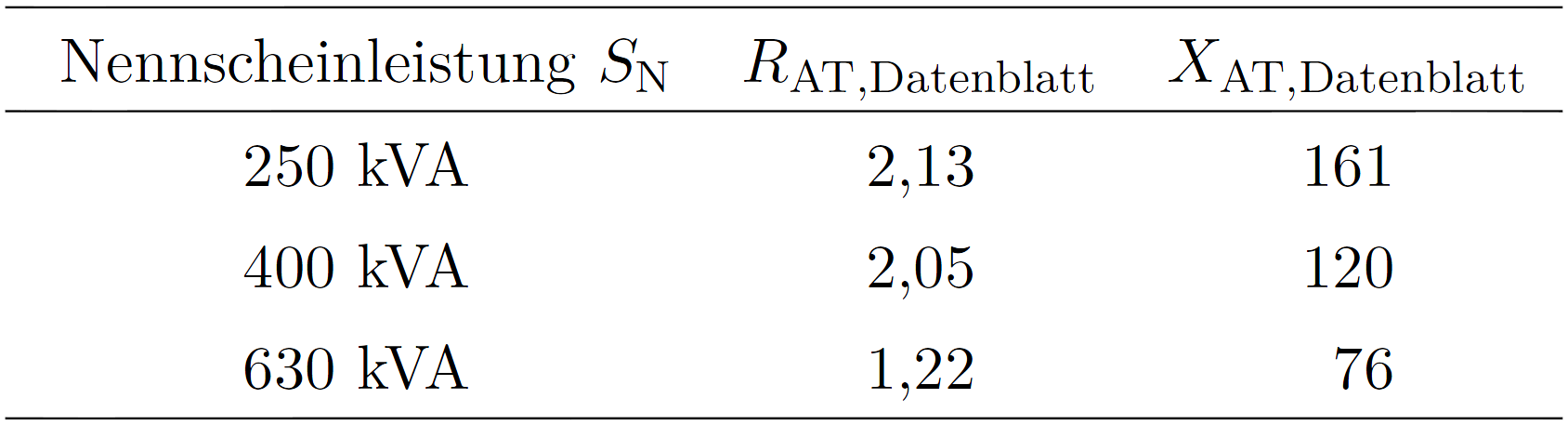
angenommen. Die Drosseln des Überschalttransformators verursachen im Vergleich zum Transformator selbst geringere Verluste. Da in der Literatur keine typischen Werte ermittelt werden konnten, wird für die Berechnungen auf die Angaben in zur Verfügung stehenden Datenblättern der J. Schneider Elektrotechnik GmbH zurückgegriffen, siehe Tabelle 2.
TABELLE 2: ANGABEN FÜR DIE ÜBERSCHALTTRANSFORMATOREN (IN ![]() )
)
Der relative Leerlaufstrom ![]() beträgt bei dem im Feldversuch in Larrieden eingesetzten 630-kVA-RONT der Siemens Transformers Austria GmbH & Co. KG sowie in einem vorliegenden Prüfbericht eines weiteren 630-kVA-RONT der Starkstrom-Gerätebau GmbH jeweils ca. 0,1 % des Nennstroms. Bei kleineren Transformatoren sind die prozentualen Werte in der Regel wohl etwas höher. Für die Berechnungen werden deshalb in der Leistungsklasse 250 kVA ein
beträgt bei dem im Feldversuch in Larrieden eingesetzten 630-kVA-RONT der Siemens Transformers Austria GmbH & Co. KG sowie in einem vorliegenden Prüfbericht eines weiteren 630-kVA-RONT der Starkstrom-Gerätebau GmbH jeweils ca. 0,1 % des Nennstroms. Bei kleineren Transformatoren sind die prozentualen Werte in der Regel wohl etwas höher. Für die Berechnungen werden deshalb in der Leistungsklasse 250 kVA ein ![]() von 0,3 % und bei 400-kVA-RONT ein
von 0,3 % und bei 400-kVA-RONT ein ![]() von 0,2 % des Nennstroms angenommen. Demzufolge sind in der neutralen Stellung die Werte für die Nennscheinleistung
von 0,2 % des Nennstroms angenommen. Demzufolge sind in der neutralen Stellung die Werte für die Nennscheinleistung ![]() , die Verlustleistungen
, die Verlustleistungen ![]() und
und ![]() , die relative Kurzschlussspannung
, die relative Kurzschlussspannung ![]() und den relativen Leerlaufstrom
und den relativen Leerlaufstrom ![]() gegeben.
gegeben.
Sonstige Positionen
Die Ersatzschaltbild-Elemente werden für alle weiteren Positionen, ausgehend von der neutralen Stellung, jeweils über die Änderung der Windungszahl ermittelt. Um den Einfluss der Stufenschalter-Position besser beurteilen zu können, bleibt bei den Berechnungen unberücksichtigt, dass laut der Ökodesign-Richtlinie der Europäischen Kommission in den Stufen 1 und 2 höhere Verluste zulässig sein können [5].
In der OS-Wicklung sind der spezifische Widerstand ![]() und der Leitungsquerschnitt
und der Leitungsquerschnitt ![]() konstant, unabhängig von der Stufenschalterstellung. Der Widerstand
konstant, unabhängig von der Stufenschalterstellung. Der Widerstand
(4) ![]()
in der OS-Wicklung ändert sich somit direkt proportional zur Windungszahl. Der Widerstand ![]() in der US-Wicklung bleibt konstant, da die US-Wicklung physisch unveränderlich ist. Der transformierte Widerstand
in der US-Wicklung bleibt konstant, da die US-Wicklung physisch unveränderlich ist. Der transformierte Widerstand
(5) ![]()
ändert sich jedoch unter Vernachlässigung des magnetischen Spannungsfalls im Eisenkern direkt proportional zum Quadrat des Übersetzungsverhältnisses. Die OS-seitige Streureaktanz
(6) ![]()
verhält sich annähernd direkt proportional zum Quadrat der Windungszahl, weil die mittlere Windungslänge ![]() näherungsweise konstant ist und die Änderungen des relativen Streuleitwertes
näherungsweise konstant ist und die Änderungen des relativen Streuleitwertes ![]() sowie des Korrekturfaktors für die Streulinienverlängerung der magnetischen Randfelder zum angrenzenden Eisen
sowie des Korrekturfaktors für die Streulinienverlängerung der magnetischen Randfelder zum angrenzenden Eisen ![]() als vernachlässigbar angenommen werden. Die US-seitige Streureaktanz
als vernachlässigbar angenommen werden. Die US-seitige Streureaktanz ![]() ist als konstant anzusehen, da sich die Windungszahl
ist als konstant anzusehen, da sich die Windungszahl ![]() nicht ändert. Ihr auf die OS-Seite transformierter Wert
nicht ändert. Ihr auf die OS-Seite transformierter Wert
(7) ![]()
ändert sich allerdings entsprechend der Transformationsvorschrift mit dem Quadrat des Übersetzungsverhältnisses. Die Hauptreaktanz
(8) ![]()
ist, ähnlich der Streureaktanz, hauptsächlich von der veränderten Windungszahl abhängig. Der formale Zusammenhang schildert sich analog zu der für die Streureaktanz ![]() genannten Erklärung. Die Eisenverluste
genannten Erklärung. Die Eisenverluste
(9) ![]()
setzen sich aus den Wirbelstromverlusten ![]() und den Hystereseverlusten
und den Hystereseverlusten ![]() zusammen und berechnen sich durch die Division des Quadrates der Oberspannung
zusammen und berechnen sich durch die Division des Quadrates der Oberspannung ![]() durch den Eisenwiderstand
durch den Eisenwiderstand ![]() . Das Quadrat des magnetischen Flusses
. Das Quadrat des magnetischen Flusses ![]()
(10) ![]()
ist proportional zum Quadrat der Induktion ![]() , welche sich wiederum proportional zum Quotient aus der Oberspannung
, welche sich wiederum proportional zum Quotient aus der Oberspannung ![]() und der OS-seitigen Wicklungszahl
und der OS-seitigen Wicklungszahl ![]() verhält. In der neutralen Position, d. h. bei vorgegebenen Werten für
verhält. In der neutralen Position, d. h. bei vorgegebenen Werten für ![]() und
und ![]() , ändert sich der Eisenwiderstand
, ändert sich der Eisenwiderstand ![]() direkt proportional zum Quadrat der Oberspannung. Bei abweichender Wicklungszahl kann
direkt proportional zum Quadrat der Oberspannung. Bei abweichender Wicklungszahl kann ![]() nur unter der Annahme bestimmt werden, dass der in der Norm DIN EN 50464 für die neutrale Position festgelegte Worst-Case-Wert von
nur unter der Annahme bestimmt werden, dass der in der Norm DIN EN 50464 für die neutrale Position festgelegte Worst-Case-Wert von ![]() auch in anderen Stufenschalter-Positionen anfällt.
auch in anderen Stufenschalter-Positionen anfällt. ![]() ist dann direkt proportional zum Quadrat der Oberspannung, während
ist dann direkt proportional zum Quadrat der Oberspannung, während ![]() wegen der Einstellung CFVV weiterhin als konstant betrachtet wird.
wegen der Einstellung CFVV weiterhin als konstant betrachtet wird.
Sobald die Spannung ![]() bei konstantem
bei konstantem ![]() variiert, kann nicht mehr von einem konstanten
variiert, kann nicht mehr von einem konstanten ![]() ausgegangen werden. Da
ausgegangen werden. Da ![]() innerhalb einer Stufenschalter-Position als konstant betrachtet wird, führt die Spannungsänderung in diesem Fall zu Änderungen von
innerhalb einer Stufenschalter-Position als konstant betrachtet wird, führt die Spannungsänderung in diesem Fall zu Änderungen von ![]() . Ein analoges Verhalten wäre bei US-geregelten RONT zu erwarten, wenn die Spannung
. Ein analoges Verhalten wäre bei US-geregelten RONT zu erwarten, wenn die Spannung ![]() bei OS-seitiger Betrachtung variiert, obwohl
bei OS-seitiger Betrachtung variiert, obwohl ![]() dann in allen Positionen unveränderlich ist.
dann in allen Positionen unveränderlich ist.
Berechnung der Ersatzschaltbild-Elemente
Zunächst müssen die Ersatzschaltbild-Elemente für die neutrale Stellung des Stufenschalters berechnet werden. Mit den gegebenen Werten für die Nennscheinleistung ![]() , die Verlustleistungen
, die Verlustleistungen ![]() und
und ![]() , die relative Kurzschlussspannung
, die relative Kurzschlussspannung ![]() und den relativen Leerlaufstrom
und den relativen Leerlaufstrom ![]() lassen sich der Nennstrom
lassen sich der Nennstrom ![]() , der Eisenverluststrom
, der Eisenverluststrom ![]() , die Kurzschlussspannung
, die Kurzschlussspannung ![]() , der Leerlaufstrom
, der Leerlaufstrom ![]() und der Magnetisierungsstrom
und der Magnetisierungsstrom ![]() mit Hilfe der Gleichungen
mit Hilfe der Gleichungen
(11) 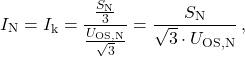
(12) 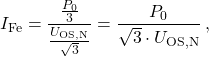
(13) ![]()
(14) ![]()
und
(15) ![]()
berechnen. Anschließend können die verbleibenden Elemente für die neutrale Position – die Hauptreaktanz ![]() , der Eisenwiderstand des Transformators
, der Eisenwiderstand des Transformators ![]() , die Kurzschlussimpedanz
, die Kurzschlussimpedanz ![]() , der Widerstand der OS-Wicklung
, der Widerstand der OS-Wicklung ![]() und die Streureaktanz der OS-Wicklung
und die Streureaktanz der OS-Wicklung ![]() – mit den Gleichungen
– mit den Gleichungen
(16) ![]()
(17) ![]()
(18) ![]()
(19) ![]()
und
(20) 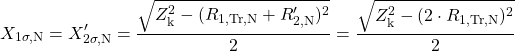
ermittelt werden. Mit Hilfe des Übersetzungsverhältnisses lässt sich zeigen, dass das Verhältnis der Windungszahl zur Nennwindungszahl
(21) 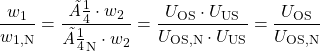
direkt proportional zum Verhältnis der Oberspannung ![]() zur Nennoberspannung
zur Nennoberspannung ![]() ist. Damit können nun die Werte für alle weiteren Positionen entsprechend den Erklärungen in Abschnitt 2.2 umgerechnet werden.
ist. Damit können nun die Werte für alle weiteren Positionen entsprechend den Erklärungen in Abschnitt 2.2 umgerechnet werden.
Außerdem fallen für den Überschalttransformator, wie im Kapitel zu den Ausführungsformen beschrieben, in allen Positionen Kupferverluste und in den Brückenpositionen aufgrund des Ausgleichsstromes zusätzlich Eisenverluste an. Die Werte für ![]() in Tabelle 2 sind für eine Serienschaltung beider Wicklungen des Überschalttransformators angegeben. Der gesamte OS-seitige Kupferwiderstand
in Tabelle 2 sind für eine Serienschaltung beider Wicklungen des Überschalttransformators angegeben. Der gesamte OS-seitige Kupferwiderstand
(22) ![]()
ergibt sich somit aus dem Widerstand ![]() der parallel geschalteten Wicklungen des Überschalttransformators und dem dazu in Reihe liegenden Widerstand
der parallel geschalteten Wicklungen des Überschalttransformators und dem dazu in Reihe liegenden Widerstand ![]() der OS-Wicklung des RONT. Der zusätzliche Eisenwiderstand
der OS-Wicklung des RONT. Der zusätzliche Eisenwiderstand
(23) 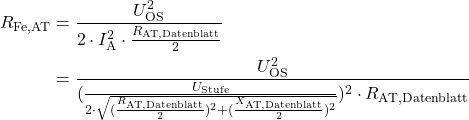
wird mit Hilfe der Näherung bestimmt, dass die vom Ausgleichsstrom verursachten Eisenverluste anfallen, wenn am Querzweig des RONT-Modells, bestehend aus Eisenwiderstand und Hauptreaktanz, die OS-seitige Spannung ![]() anliegt. Für die Modellbildung wird in den Brückenpositionen der Widerstand
anliegt. Für die Modellbildung wird in den Brückenpositionen der Widerstand ![]() parallel zum Eisenwiderstand
parallel zum Eisenwiderstand ![]() des Transformators geschaltet, wodurch sich bei einer gegebenen Spannung
des Transformators geschaltet, wodurch sich bei einer gegebenen Spannung ![]() wie erwartet größere Verluste am Eisenwiderstand
wie erwartet größere Verluste am Eisenwiderstand
(24) ![]()
einstellen.
Berechnungsergebnisse für typische RONT-Modelle
Abschließend werden die Ersatzschaltbild-Elemente der RONT mit Hilfe von typischen Auslegungswerten berechnet, um den Einfluss der Stufenschalter-Positionen anhand von Zahlenwerten besser beurteilen zu können. Tabelle 3 zeigt eine Übersicht der Auslegungswerte, welche sich nach verfügbaren Ausführungsbeispielen des GRIDCON![]() richten. Die relativen Leerlaufströme
richten. Die relativen Leerlaufströme ![]() beruhen, wie im Abschnitt 2.1 beschrieben, für den 630-kVA-RONT auf vorhandenen Prüfberichten und für die 250- und 400-kVA-RONT auf daraus abgeleiteten Schätzwerten. Die Verlustklassen entsprechen den Ökodesign-Anforderungen der Europäischen Union an dreiphasige flüssigkeitsgefüllte Mittelleistungstransformatoren, die nach dem 1. Juli 2015 bzw. nach dem 1. Juli 2021 beschafft werden [5].
beruhen, wie im Abschnitt 2.1 beschrieben, für den 630-kVA-RONT auf vorhandenen Prüfberichten und für die 250- und 400-kVA-RONT auf daraus abgeleiteten Schätzwerten. Die Verlustklassen entsprechen den Ökodesign-Anforderungen der Europäischen Union an dreiphasige flüssigkeitsgefüllte Mittelleistungstransformatoren, die nach dem 1. Juli 2015 bzw. nach dem 1. Juli 2021 beschafft werden [5].
TABELLE 3: TYPISCHE AUSLEGUNGSWERTE VON RONT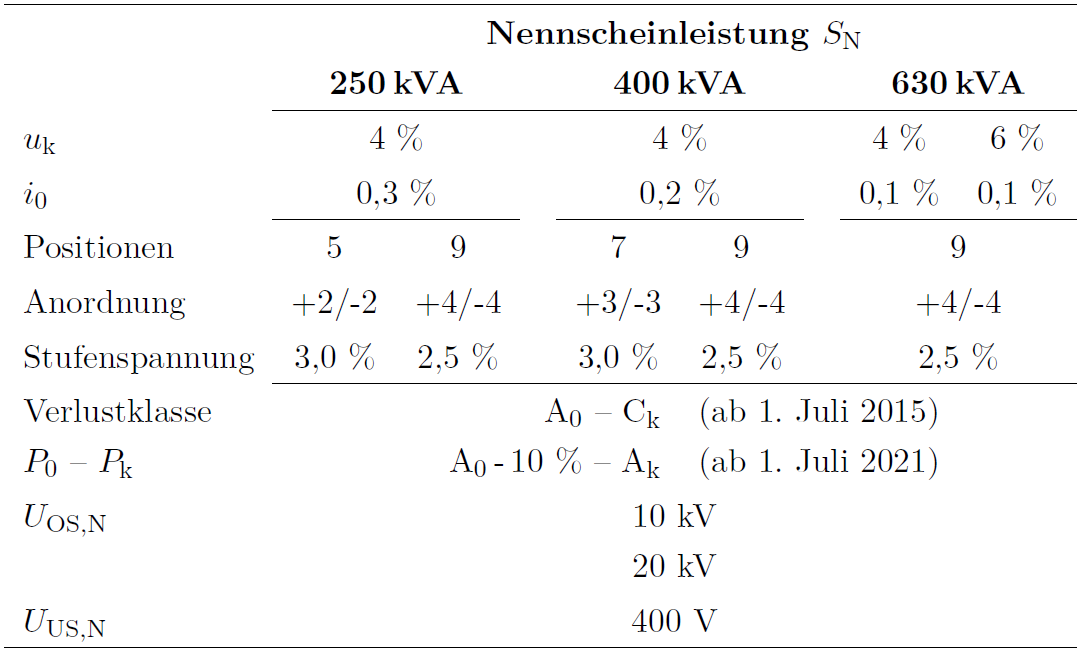
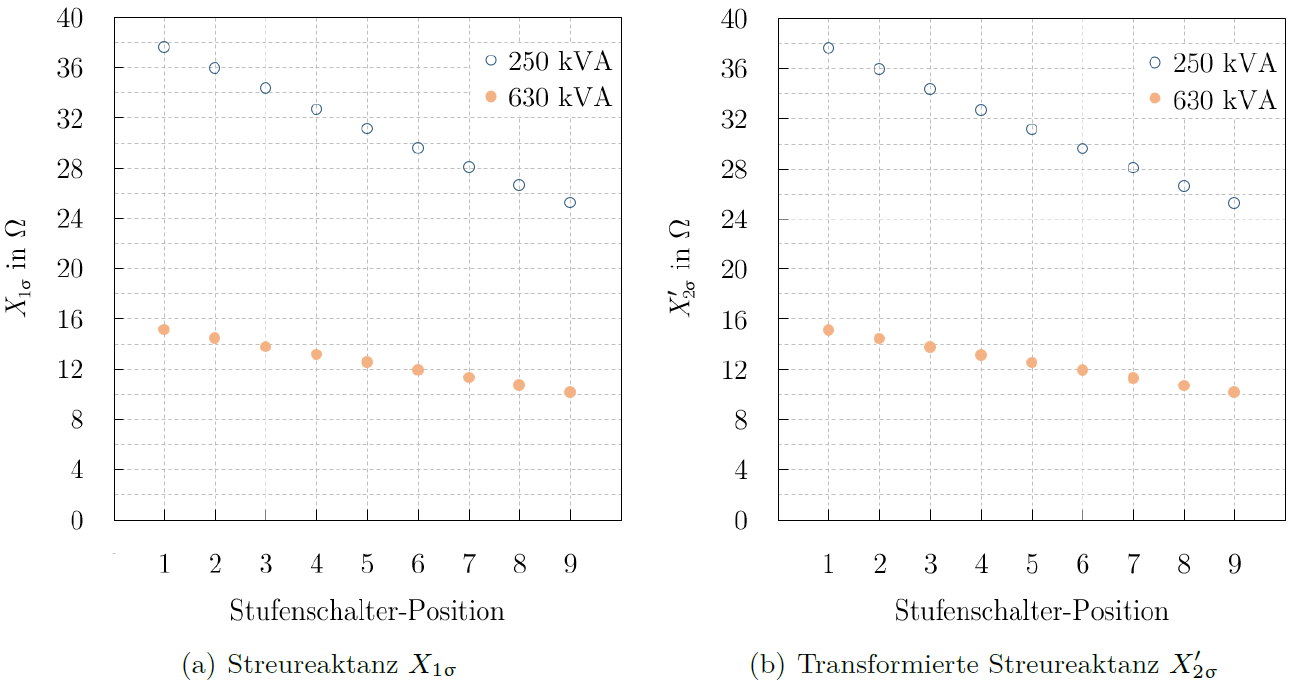
Zur graphischen Veranschaulichung der Ergebnisse zeigen Abbildungen 3-5 jeweils einen Vergleich der berechneten Werte für einen 250- und 630-kVA-GRIDCON![]() , beide mit 9 Stufenschalter-Positionen,
, beide mit 9 Stufenschalter-Positionen, ![]() = 4 %, Verlustklasse
= 4 %, Verlustklasse ![]() – 10 % –
– 10 % – ![]() und
und ![]() = 20 kV.
= 20 kV.
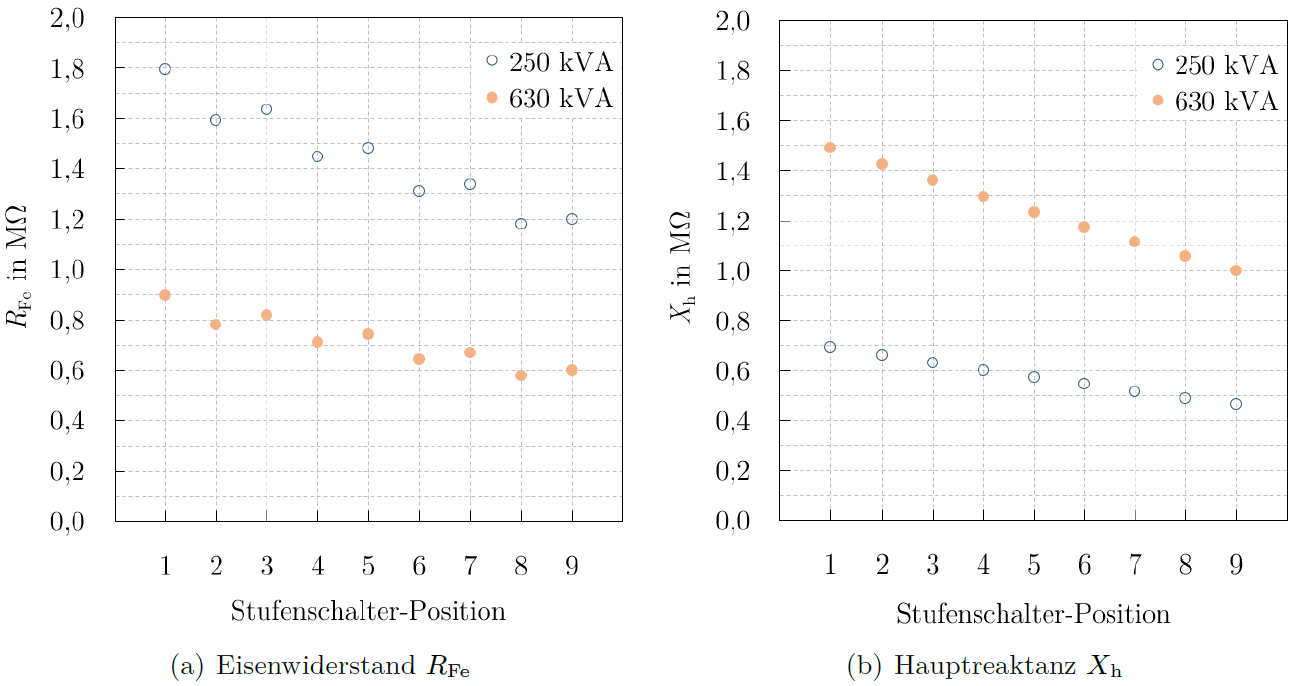
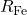 und Hauptreaktanz
und Hauptreaktanz 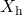 für einen 250- und 630-kVA-GRIDCON
für einen 250- und 630-kVA-GRIDCON
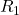 und
und 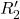 für einen 250- und 630-kVA-GRIDCON
für einen 250- und 630-kVA-GRIDCON
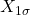 und
und 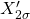 für einen 250- und 630-kVA-GRIDCON
für einen 250- und 630-kVA-GRIDCON
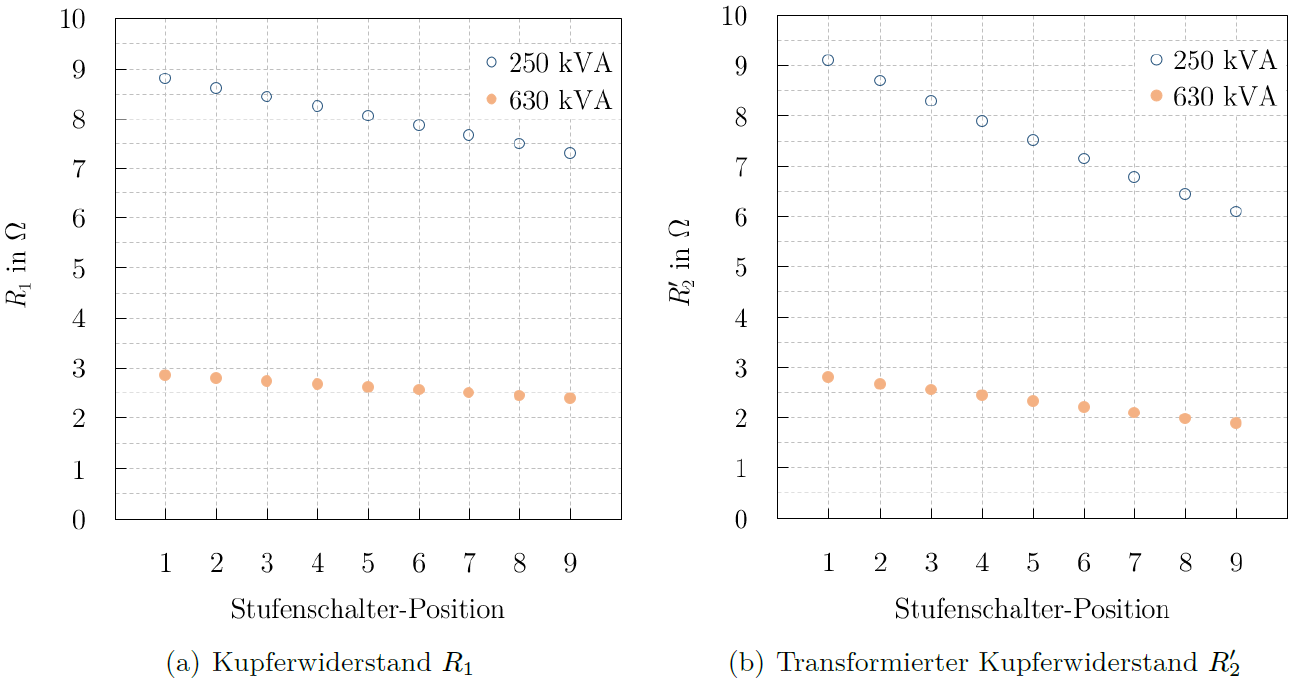
Die sprunghaften Änderungen des Eisenwiderstands ![]() in Abbildung 3 (a) ergeben sich durch den Einfluss des Überschalttransformators in den Brückenpositionen. Zum Teil zeigen die berechneten Werte deutliche Abweichungen zwischen der neutralen Stellung des RONT und den Positionen mit der kleinsten bzw. größten Windungszahl. In Tabelle 4 sind die maximalen prozentualen Abweichungen in Abhängigkeit von der Nennoberspannung
in Abbildung 3 (a) ergeben sich durch den Einfluss des Überschalttransformators in den Brückenpositionen. Zum Teil zeigen die berechneten Werte deutliche Abweichungen zwischen der neutralen Stellung des RONT und den Positionen mit der kleinsten bzw. größten Windungszahl. In Tabelle 4 sind die maximalen prozentualen Abweichungen in Abhängigkeit von der Nennoberspannung ![]() und der Anzahl an möglichen Positionen aufgelistet.
und der Anzahl an möglichen Positionen aufgelistet.
TABELLE 4: MAXIMALE ABWEICHUNGEN ZUR NEUTRALEN POSITION (IN %)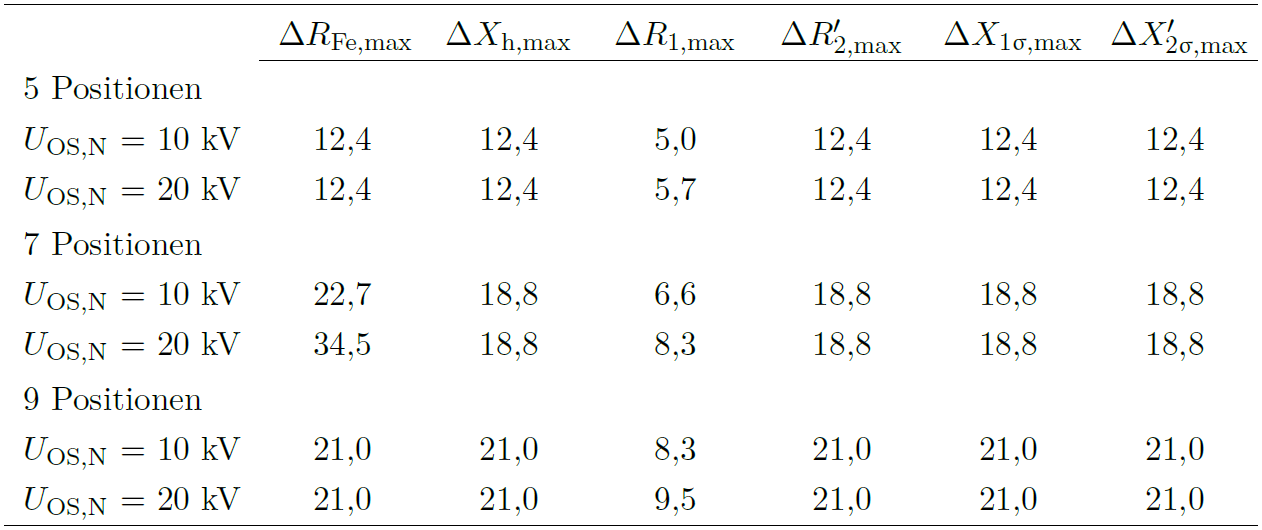
Die prozentuale Abweichung des Widerstandes ![]() fällt kleiner aus als bei den anderen Ersatzschaltbild-Elementen. Dies erklärt sich durch die lineare (statt quadratische) Abhängigkeit von der Windungszahl
fällt kleiner aus als bei den anderen Ersatzschaltbild-Elementen. Dies erklärt sich durch die lineare (statt quadratische) Abhängigkeit von der Windungszahl ![]() . Zudem stellen sich bei einer Nennoberspannung von 20 kV größere Abweichungen von
. Zudem stellen sich bei einer Nennoberspannung von 20 kV größere Abweichungen von ![]() als bei 10 kV heraus. Zur Begründung kann wiederum auf den Einfluss des Überschalttransformators verwiesen werden, da die in jeder Position addierten Zusatzwiderstände
als bei 10 kV heraus. Zur Begründung kann wiederum auf den Einfluss des Überschalttransformators verwiesen werden, da die in jeder Position addierten Zusatzwiderstände ![]() eine Verkleinerung der prozentualen Abweichung bewirken. Bei den für
eine Verkleinerung der prozentualen Abweichung bewirken. Bei den für ![]() = 20 kV vergleichsweise größeren Widerständen
= 20 kV vergleichsweise größeren Widerständen ![]() fällt diese Reduktion geringer aus und die prozentuale Abweichung erscheint größer als bei
fällt diese Reduktion geringer aus und die prozentuale Abweichung erscheint größer als bei ![]() = 10 kV.
= 10 kV.
Außerdem ist zu erkennen, dass die maximalen Abweichungen mit steigender Anzahl von Positionen tendenziell zunimmt. Dieser Zusammenhang ergibt sich durch den größeren Bereich der wählbaren Windungszahlen bei RONT mit größerer Anzapfungsanzahl.
Die höchsten Abweichungen zeigen sich beim Widerstand ![]() bei einem RONT mit 7 Positionen. Bei diesem Modell fällt die neutrale Stellung auf eine Brückenposition (vgl. Tabelle 1), wodurch sich der Eisenwiderstand durch den Einfluss des Überschalttransformators verkleinert. In Position 1 fließt kein Ausgleichsstrom und der Eisenwiderstand bleibt unverändert hoch. Daraus folgt eine relativ große Differenz zwischen beiden Werten. Die Abweichungen für unterschiedliche Nennoberspannungen erklären sich durch die in den Brückenpositionen parallel geschalteten Zusatzwiderstände
bei einem RONT mit 7 Positionen. Bei diesem Modell fällt die neutrale Stellung auf eine Brückenposition (vgl. Tabelle 1), wodurch sich der Eisenwiderstand durch den Einfluss des Überschalttransformators verkleinert. In Position 1 fließt kein Ausgleichsstrom und der Eisenwiderstand bleibt unverändert hoch. Daraus folgt eine relativ große Differenz zwischen beiden Werten. Die Abweichungen für unterschiedliche Nennoberspannungen erklären sich durch die in den Brückenpositionen parallel geschalteten Zusatzwiderstände ![]() , welche für beide Spannungen als gleich groß angenommen werden und sich deshalb bei
, welche für beide Spannungen als gleich groß angenommen werden und sich deshalb bei ![]() = 20 kV stärker auswirken.
= 20 kV stärker auswirken.
Quellen
[1] Norm DIN EN 50464 Teil 1 Dezember 2007. Ölgefüllte Drehstrom-Verteilungstransformatoren 50 Hz, 50 kVA bis 2500 kVA mit einer höchsten Spannung für Betriebsmittel bis 36 kV : Allgemeine Anforderungen.
[2] Norm DIN EN 60076 Teil 1 Dezember 1997. Leistungstransformatoren : Allgemeines.
[3] Küchler, Rudolf: Die Transformatoren. Grundlagen für ihre Berechnung und Konstruktion. Berlin : Springer, 1956.
[4] Heuck, Klaus; Dettmann, Klaus-Dieter: Elektrische Energieversorgung. Erzeugung, Transport und Verteilung elektrischer Energie – für Studium und Praxis. 5. Aufl. Braunschweig : Vieweg, 2002.
[5] Verordnung (EU) Nr. 548/2014 der Kommission vom 21. Mai 2014 zur Umsetzung der Richtlinie 2009/125/EG des Europäischen Parlaments und des Rates hinsichtlich Kleinleistungs-, Mittelleistungs- und Großleistungstransformatoren.